题目内容
已知正四面体的高为4,则此正四面体的内切球的表面积为 .
考点:球的体积和表面积,球内接多面体
专题:空间位置关系与距离
分析:作出正四面体的图形,球的球心位置为O,说明OE是内切球的半径,再求表面积.
解答:
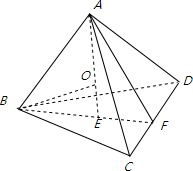 解:如图O为正四面体ABCD的内切球的球心,正四面体的高AE=4;
解:如图O为正四面体ABCD的内切球的球心,正四面体的高AE=4;
所以OE为内切球的半径,OE=
AE=1,
则其内切球的半径是1,
内切球的表面积为4π;
故答案为:4π.
 解:如图O为正四面体ABCD的内切球的球心,正四面体的高AE=4;
解:如图O为正四面体ABCD的内切球的球心,正四面体的高AE=4;所以OE为内切球的半径,OE=
| 1 |
| 4 |
则其内切球的半径是1,
内切球的表面积为4π;
故答案为:4π.
点评:本题考查正四面体的内切球半径的求法,内切球的半径是正四面体的高的
,是中档题,解题时要认真审题,注意空间思维能力的培养.
| 1 |
| 4 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数①y=3x;②y=lnx;③y=x-1;④y=x
.则下列函数图象(在第一象限部分)从左到右依次与函数序号的对应顺序一致的是( )
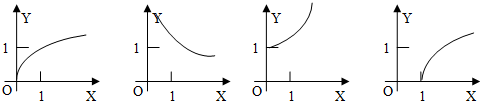
| 1 |
| 2 |
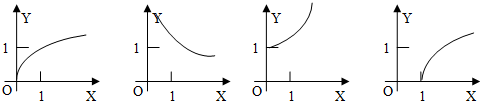
| A、④③①② | B、②③①④ |
| C、④①③② | D、②①③④ |