题目内容
8.等比数列{an}的各项均为实数,其前n项为Sn,已知S3=$\frac{7}{4}$,S6=$\frac{63}{4}$,则a8=32.分析 设等比数列{an}的公比为q≠1,S3=$\frac{7}{4}$,S6=$\frac{63}{4}$,可得$\frac{{a}_{1}(1-{q}^{3})}{1-q}$=$\frac{7}{4}$,$\frac{{a}_{1}(1-{q}^{6})}{1-q}$=$\frac{63}{4}$,联立解出即可得出.
解答 解:设等比数列{an}的公比为q≠1,
∵S3=$\frac{7}{4}$,S6=$\frac{63}{4}$,∴$\frac{{a}_{1}(1-{q}^{3})}{1-q}$=$\frac{7}{4}$,$\frac{{a}_{1}(1-{q}^{6})}{1-q}$=$\frac{63}{4}$,
解得a1=$\frac{1}{4}$,q=2.
则a8=$\frac{1}{4}×{2}^{7}$=32.
故答案为:32.
点评 本题考查了等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
18.已知复数z满足z(1+i)=2i,则z的共轭复数$\overline{z}$等于( )
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
16.函数f(x)=sin(2x+$\frac{π}{3}$)的最小正周期为( )
| A. | 4π | B. | 2π | C. | π | D. | $\frac{π}{2}$ |
3.某工厂生产甲、乙、丙、丁四种不同型号的产品,产量分别为200,400,300,100件.为检验产品的质量,现用分层抽样的方法从以上所有的产品中抽取60件进行检验,则应从丙种型号的产品中抽取18件.
20.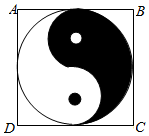 如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )
如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )
 如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )
如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{π}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{π}{4}$ |
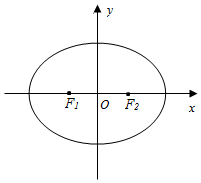 如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,离心率为$\frac{1}{2}$,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1,过点F2作直线PF2的垂线l2.
如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,离心率为$\frac{1}{2}$,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1,过点F2作直线PF2的垂线l2.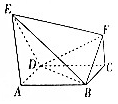 如图,正方形ABCD的边长为1,E,F是平面ABCD同一侧的两点,AE∥FC,AE⊥AB,AE=1,DE=$\sqrt{2}$,FC=$\frac{1}{2}$.
如图,正方形ABCD的边长为1,E,F是平面ABCD同一侧的两点,AE∥FC,AE⊥AB,AE=1,DE=$\sqrt{2}$,FC=$\frac{1}{2}$.