题目内容
3.某工厂生产甲、乙、丙、丁四种不同型号的产品,产量分别为200,400,300,100件.为检验产品的质量,现用分层抽样的方法从以上所有的产品中抽取60件进行检验,则应从丙种型号的产品中抽取18件.分析 由题意先求出抽样比例即为$\frac{6}{100}$,再由此比例计算出应从丙种型号的产品中抽取的数目.
解答 解:产品总数为200+400+300+100=1000件,而抽取60件进行检验,抽样比例为$\frac{60}{1000}$=$\frac{6}{100}$,
则应从丙种型号的产品中抽取300×$\frac{6}{100}$=18件,
故答案为:18
点评 本题的考点是分层抽样.分层抽样即要抽样时保证样本的结构和总体的结构保持一致,按照一定的比例,即样本容量和总体容量的比值,在各层中进行抽取.

练习册系列答案
相关题目
13.下列命题为真命题的是( )
| A. | 若p∧q为假命题,则p∨q为真命题 | |
| B. | 不存在实数α,β,使得等式tanα+tanβ=tan(α+β)成立 | |
| C. | 函数f(x)=ax2+bx+c为偶函数的充要条件是 b=0 | |
| D. | 若定义在R上的函数f(x)满足f(x)•f(x+1)=1,则f(x)是一个周期为1的函数 |
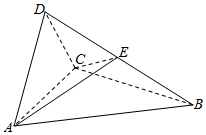 如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.  如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°,E是PD的中点.
如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°,E是PD的中点.