题目内容
在数列{an}中,a1=3,an=2an-1+n-2(n≥2,且n∈N*)
(Ⅰ)求a2,a3的值;
(Ⅱ)证明:数列{an+n}是等比数列,并求{an}的通项公式.
(Ⅰ)求a2,a3的值;
(Ⅱ)证明:数列{an+n}是等比数列,并求{an}的通项公式.
考点:数列递推式
专题:等差数列与等比数列
分析:(I)赋值:令n=2,n=3,能求出a2,a3的值.
(II)涉及到等差数列,等比数列的证明问题,只需按照定义证明即可,利用等比数列的定义证明,利用等比数列通项公式可求出{an+n}的通项公式,从而求出an.
(II)涉及到等差数列,等比数列的证明问题,只需按照定义证明即可,利用等比数列的定义证明,利用等比数列通项公式可求出{an+n}的通项公式,从而求出an.
解答:
解:(I)令n=2,得a2=2a1=6,
令n=3,得a3=2a2+1=13.(4分)
(II)∵
=
=2,
∴数列{an+n}是首项为4,公比为2的等比数列,(7分)
∴an+n=4•2n-1=2n+1,
∴an=2n+1-n.(10分)
令n=3,得a3=2a2+1=13.(4分)
(II)∵
| an+n |
| an-1+(n-1) |
| 2an-1+n-2+n |
| an-1+n-1 |
∴数列{an+n}是首项为4,公比为2的等比数列,(7分)
∴an+n=4•2n-1=2n+1,
∴an=2n+1-n.(10分)
点评:本题考查等比数列的证明,考查数列的通项公式的求法,是中档题,解题时要注意赋值法和等比数列性质的合理运用.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
已知一个算法的程序框图如图所示,当输出的结果为0时,输入的x的值为( )


| A、1 | B、-2 |
| C、1或-1 | D、1或-2 |
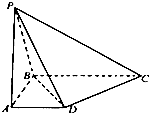 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=1,BC=2,又PB=1,∠PBC=120°,AB⊥PC,直线AB与直线PD所成的角为60°.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=1,BC=2,又PB=1,∠PBC=120°,AB⊥PC,直线AB与直线PD所成的角为60°.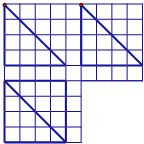 如图在边长为1的正方形网格中用粗线画出了某个多面体的三视图,则该多面体的外接球的体积为
如图在边长为1的正方形网格中用粗线画出了某个多面体的三视图,则该多面体的外接球的体积为