Question

设数列{a_n}的前n项和为S_n，a₁＝1，a_n＝＋2 (n－1) (n∈N^*)．

(1)求证：数列{a_n}为等差数列，并分别写出a_n和S_n关于n的表达式；

(2)是否存在自然数n，使得S₁＋＋＋…＋－(n－1)²＝2 013？若存在，求出n的值；若不存在，请说明理由．

（3）设,，是否存在最大的整数m，使得对任意n∈N^*均有T_n＞成立？若存在，求出m的值；若不存在，说明理由.

Answer 1

解　(1)由a_n＝＋2(n－1)，得S_n＝na_n－2n(n－1) (n∈N^*)．

当n≥2时，a_n＝S_n－S_n－1＝na_n－(n－1)a_n－1－4(n－1)，

即a_n－a_n－1＝4，故数列{a_n}是以1为首项，以4为公差的等差数列．

于是，a_n＝4n－3，S_n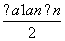＝＝2n²－n (n∈N^*)．

(2)由S_n＝na_n－2n(n－1)，得＝2n－1 (n∈N^*)，

又S₁＋＋＋…＋－(n－1)²＝1＋3＋5＋7＋…＋(2n－1)－(n－1)²＝n²－(n－1)²＝2n－1.

令2n－1＝2 013，得n＝1 007，即存在满足条件的自然数n＝1 007.

（3）

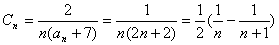
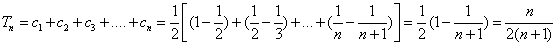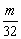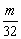要使T_n＞总成立，需＜T₁=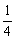成立，即m＜8且m∈Z，故适合条件的m的最大值为7.