题目内容
棱长为2的四棱锥底面ABCD是正方形,将侧面PBC水平放置,则这个几何体的三视图中,俯视图的面积为 .
考点:简单空间图形的三视图
专题:空间位置关系与距离
分析:根据已知画出侧面PBC水平放置时,几何体的俯视图,并求出相应的边长,代入矩形和三角形面积公式后可得答案.
解答:
解:作棱锥的轴截面(其中E,F为底面对边AD和BC的中点,O为底面中心),如下图所示:
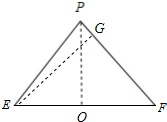
∵则四棱锥的棱长为2,
∴EF=2,PE=PF=
,PO=
,
作EG⊥PF,垂足为G,则EG=
=
,PG=
=
,
将侧面PBC水平放置后,棱锥的俯视图如图所示,
则△PBC是等边三角形,PE=
,

∴FG=PF-PG=
-
=
,
∴俯视图面积=2×
+
×2×
=
,
故答案为:
.

∵则四棱锥的棱长为2,
∴EF=2,PE=PF=
| 3 |
| 2 |
作EG⊥PF,垂足为G,则EG=
| PO•EF |
| PF |
2
| ||
| 3 |
| PE2-EG2 |
| ||
| 3 |
将侧面PBC水平放置后,棱锥的俯视图如图所示,
则△PBC是等边三角形,PE=
| 3 |

∴FG=PF-PG=
| 3 |
| ||
| 3 |
2
| ||
| 3 |
∴俯视图面积=2×
2
| ||
| 3 |
| 1 |
| 2 |
| ||
| 3 |
5
| ||
| 3 |
故答案为:
5
| ||
| 3 |
点评:本题考查的知识点是简单几何体的三视图,其中画出满足条件的图形是解答的关键.

练习册系列答案
相关题目

 若x∈(-
若x∈(-