题目内容
11．已知函数f（x）=$\frac{{e}^{2x}+1}{{e}^{2x}-1}$，则y=f（x）的大致图象为（ ）| A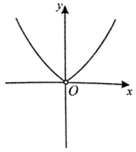． |  | B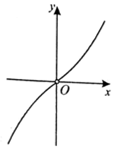． |  | C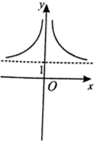． |  | D． |  |
分析 化简解析式，利用函数的单调性，判断函数的图象即可．
解答 解：函数f（x）=$\frac{{e}^{2x}+1}{{e}^{2x}-1}$=1+$\frac{2}{{e}^{2x}-1}$，因为函数y=e2x是增函数，所以函数f（x）=$\frac{{e}^{2x}+1}{{e}^{2x}-1}$，x＞0时是减函数，
可知函数的图象只有D满足题意．
故选：D．
点评 本题考查函数的图象的判断，函数的单调性的应用，考查计算能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
1．过点P（1，0）与抛物线y=x2有且只有一个公共点的直线共有（ ）
| A． | 4条 | B． | 3条 | C． | 2条 | D． | 1条 |
6．定义在R上的周期为2的函数，满足f（2+x）=f（2-x），在[-3，-2]上是减函数，若A，B是锐角三角形的两个内角，则（ ）
| A． | f（sinA）＞f（cosB） | B． | f（cosB）＞f（sinA） | C． | f（sinA）＞f（sinB） | D． | f（cosB）＞f（cosA） |
16．设D、E、F分别为△ABC三边BC、CA、AB的中点，则$\overrightarrow{DA}$+2$\overrightarrow{EB}$+3$\overrightarrow{FC}$=（ ）
| A． | $\frac{1}{2}$$\overrightarrow{AD}$ | B． | $\frac{3}{2}$$\overrightarrow{AD}$ | C． | $\frac{1}{2}$$\overrightarrow{AC}$ | D． | $\frac{3}{2}$$\overrightarrow{AC}$ |