Question

一椭圆的四个顶点为A₁B₁A₂B₂，以椭圆的中心为圆心的圆过椭圆的焦点且与菱形A₁B₁A₂B₂相切，则椭圆的离心率为

5 -1

2

．

Answer 1

分析：可得椭圆的中心到直线A₂B₂的距离为c，结合b²=a²-c²可得关于ac的方程，由离心率的定义解方程可得．

解答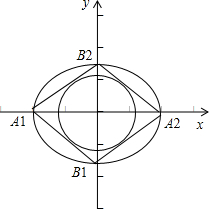：解：由题意可得椭圆的中心O（0，0）到直线A₂B₂的距离为c，
可得直线A₂B₂的方程为

x

a

+

y

b

=1，即bx+ay-ab=0，
由点到直线的距离公式可得

|ab|

b2+a2

=c，
变形可得a²b²=c²（a²+b²），由b²=a²-c²可得
a²（a²-c²）=c²（2a²-c²），即a⁴-3a²c²+c⁴=0，
两边同除以a⁴可得1-3e²+e⁴=0，
解得e²=

3± 5

2

，结合e∈（0，1）可得e=

5 -1

2

故答案为：

5 -1

2

点评：本题考查椭圆离心率的求解，涉及点到直线的距离公式和一元二次方程的求解，属中档题．