题目内容
(2012•淄博二模)已知椭圆C:
+
=1(a>b>0)的离心率e=
,连接椭圆的四个顶点得到的菱形的面积为4
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)圆x2+y2=1的一条切线l与椭圆C相交于A,B两点,问是否存在上述直线l使
•
=0成立?若存在,求出直线l的方程;若不存在,请说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)圆x2+y2=1的一条切线l与椭圆C相交于A,B两点,问是否存在上述直线l使
| OA |
| OB |
分析:(Ⅰ)由e=
,得a2=4c2,再由c2=a2-b2,解得a=
b,利用连接椭圆的四个顶点得到的菱形的面积为4
,即可求得椭圆的方程;
(Ⅱ)假设存在直线l满足条件
①当直线l的斜率不存在时,则方程为x=±1,可得
•
=0不成立;
②斜率存在时,假设方程为y=kx+m,由直线与圆相切可得m2=1+k2,直线方程代入椭圆方程,利用韦达定理,结合向量的数量积运算,即可得到结论.
| 1 |
| 2 |
2
| ||
| 3 |
| 3 |
(Ⅱ)假设存在直线l满足条件
①当直线l的斜率不存在时,则方程为x=±1,可得
| OA |
| OB |
②斜率存在时,假设方程为y=kx+m,由直线与圆相切可得m2=1+k2,直线方程代入椭圆方程,利用韦达定理,结合向量的数量积运算,即可得到结论.
解答:解:(Ⅰ)由e=
,得a2=4c2,再由c2=a2-b2,解得a=
b①.
由连接椭圆的四个顶点得到的菱形的面积为4
,可知2ab=4
②.
①②可得a=2,b=
.
所以椭圆的方程为
+
=1.
(Ⅱ)假设存在直线l满足条件
①当直线l的斜率不存在时,则方程为x=±1
当方程为x=1时,直线l与椭圆的交点为A(1,
),B(1,-
),则
•
=1-
=-
≠0
同理方程为x=1时,
•
=0也不成立;
②斜率存在时,假设方程为y=kx+m,由直线与圆相切可得m2=1+k2,
直线方程代入椭圆方程,消去y,可得(3+4k2)x2+8kmx+4m2-12=0
设A(x1,y1),B(x2,y2),则x1+x2=-
,x1x2=
∴y1y2=(kx1+m)(kx2+m)=
∴
•
=x1x2+y1y2=
+
=
<0
综上所述,直线l不存在.
| 1 |
| 2 |
2
| ||
| 3 |
由连接椭圆的四个顶点得到的菱形的面积为4
| 3 |
| 3 |
①②可得a=2,b=
| 3 |
所以椭圆的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)假设存在直线l满足条件
①当直线l的斜率不存在时,则方程为x=±1
当方程为x=1时,直线l与椭圆的交点为A(1,
| 3 |
| 2 |
| 3 |
| 2 |
| OA |
| OB |
| 9 |
| 4 |
| 5 |
| 4 |
同理方程为x=1时,
| OA |
| OB |
②斜率存在时,假设方程为y=kx+m,由直线与圆相切可得m2=1+k2,
直线方程代入椭圆方程,消去y,可得(3+4k2)x2+8kmx+4m2-12=0
设A(x1,y1),B(x2,y2),则x1+x2=-
| 8km |
| 3+4k2 |
| 4m2-12 |
| 3+4k2 |
∴y1y2=(kx1+m)(kx2+m)=
| 3m2-12k2 |
| 3+4k2 |
∴
| OA |
| OB |
| 4m2-12 |
| 3+4k2 |
| 3m2-12k2 |
| 3+4k2 |
| -5(k2+1) |
| 3+4k2 |
综上所述,直线l不存在.
点评:本题考查椭圆的标准方程,考查直线与圆,直线与椭圆的位置关系,考查向量的数量积运算,属于中档题.

练习册系列答案
相关题目
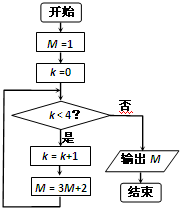 (2012•淄博二模)执行如图所示的程序框图,输出的M的值为( )
(2012•淄博二模)执行如图所示的程序框图,输出的M的值为( )