题目内容
6.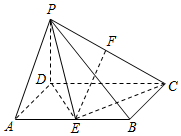 如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=2AD,PD⊥底面ABCD,E,F分别为棱AB,PC的中点.
如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=2AD,PD⊥底面ABCD,E,F分别为棱AB,PC的中点.(1)求证:EF∥平面PAD;
(2)求证:平面PDE⊥平面PEC.
分析 (1)取PD的中点G,连接AG,FG,则由中位线定理可知四边形AEFG是平行四边形,于是EF∥AG,从而得出EF∥平面PAD;
(2)由PD⊥平面ABCD得出PD⊥CE,由勾股定理的逆定理得出CE⊥DE,于是CE⊥平面PDE,故而平面PDE⊥平面PEC.
解答 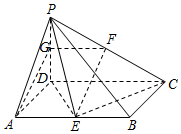 证明:(1)取PD的中点G,连接AG,FG.
证明:(1)取PD的中点G,连接AG,FG.
∵F,G分别是PC,PD的中点,
∴GF∥DC,GF=$\frac{1}{2}$DC,
又E是AB的中点,
∴AE∥DC,且AE=$\frac{1}{2}$DC,
∴GF∥AE,且GF=AE,
∴四边形AEFG是平行四边形,故EF∥AG.
又EF?平面PAD,AG?平面PAD,
∴EF∥平面PAD.
(2)∵PD⊥底面ABCD,EC?底面ABCD,
∴CE⊥PD.
∵四边形ABCD是矩形,AB=2AD,
∴DE=$\sqrt{2}$AD,CE=$\sqrt{2}$AD,CD=2AD,
∴DE2+CE2=CD2,即CE⊥DE,
又PD?平面PDE,DE?平面PDE,PD∩DE=D,
∴CE⊥平面PDE.
∵CE?平面PEC,
∴平面PDE⊥平面PEC.
点评 本题考查了线面平行,面面垂直的判定,属于中档题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
16.设x,y满足约束条件$\left\{\begin{array}{l}{y≤2x}\\{x+y≤1}\\{y+1≥0}\end{array}\right.$,则z=x+3y的最大值是( )
| A. | $\frac{4}{3}$ | B. | $\frac{7}{3}$ | C. | -$\frac{1}{3}$ | D. | 1 |
11.在空间中,下列结论正确的是( )
| A. | 空间三点确定一个平面 | |
| B. | 过直线外一点有且只有一条直线与已知直线垂直 | |
| C. | 如果一条直线与平面内的一条直线平行,则这条直线与平面平行 | |
| D. | 三个平面最多将可空间分成八块 |
15.已知实数a>0,b>0,0<m<4,且a+b=2,则$\frac{1}{a}$+$\frac{4}{(4-m)b}$+$\frac{4}{mb}$的最小值为( )
| A. | 4 | B. | $\frac{9}{2}$ | C. | 5 | D. | 6 |