题目内容
15.已知实数a>0,b>0,0<m<4,且a+b=2,则$\frac{1}{a}$+$\frac{4}{(4-m)b}$+$\frac{4}{mb}$的最小值为( )| A. | 4 | B. | $\frac{9}{2}$ | C. | 5 | D. | 6 |
分析 由$\frac{1}{a}$+$\frac{4}{(4-m)b}$+$\frac{4}{mb}$=$\frac{1}{a}$+$\frac{4}{b}$($\frac{1}{4-m}$+$\frac{1}{m}$),先根据基本不等式求出$\frac{1}{4-m}$+$\frac{1}{m}$=$\frac{4}{m(4-m)}$的最小值,再代入去求$\frac{1}{a}$+$\frac{4}{b}$=$\frac{1}{2}$($\frac{1}{a}$+$\frac{4}{b}$)(a+b)的最小值,问题得以解决.
解答 解:∵$\frac{1}{a}$+$\frac{4}{(4-m)b}$+$\frac{4}{mb}$=$\frac{1}{a}$+$\frac{4}{b}$($\frac{1}{4-m}$+$\frac{1}{m}$)
∵0<m<4,
∴m(4-m)≤($\frac{m+4-m}{2}$)2=4,当且仅当m=2时等号成立,
∴$\frac{1}{4-m}$+$\frac{1}{m}$=$\frac{m+4-m}{m(4-m)}$=$\frac{4}{m(4-m)}$≥$\frac{4}{4}$=1,
∵a>0,b>0,且a+b=2,
∴$\frac{1}{a}$+$\frac{4}{(4-m)b}$+$\frac{4}{mb}$≥$\frac{1}{a}$+$\frac{4}{b}$=$\frac{1}{2}$($\frac{1}{a}$+$\frac{4}{b}$)(a+b)=$\frac{1}{2}$(1+4+$\frac{b}{a}$+$\frac{4a}{b}$)≥$\frac{1}{2}$(5+2$\sqrt{\frac{b}{a}•\frac{4a}{b}}$)=$\frac{9}{2}$,当且仅当a=$\frac{2}{3}$,b=$\frac{4}{3}$时取等号,
∴$\frac{1}{a}$+$\frac{4}{(4-m)b}$+$\frac{4}{mb}$的最小值为$\frac{9}{2}$,
故选:B.
点评 本题考查了基本不等式的应用,关键是灵活构造基本不等式,并注意不等号成立的条件,属于中档题.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案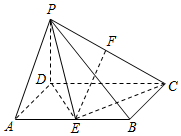 如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=2AD,PD⊥底面ABCD,E,F分别为棱AB,PC的中点.
如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=2AD,PD⊥底面ABCD,E,F分别为棱AB,PC的中点.