题目内容
1.△ABC是正三角形,平面ABC外有一点O,且OA=OB=OC,截面PQRS平行于OA和BC,则四边形PQRS是距形.分析 由条件可知三棱锥的正三棱锥,作三棱锥的高线OO′,则可证BC⊥平面OAO′,于是BC⊥OA,由线面平行的性质可得截面四边形为平行四边形,由于四边形的两邻边分别与OA,BC平行,故而四边形的两邻边互相垂直.
解答  解:∵△ABC是正三角形,且OA=OB=OC,
解:∵△ABC是正三角形,且OA=OB=OC,
∴三棱锥O-ABC为正三棱锥,
∵OA∥平面PQRS,OA?平面OAC,平面OAC∩平面PQRS=RS,
∴RS∥OA,
同理可得OA∥PQ,BC∥PS,BC∥QR,
∴RS∥PQ,RQ∥PS,
∴四边形PQRS是平行四边形.
作OO′⊥平面ABC,则O′为△ABC的中心,连结AO′并延长交BC与D,则AD⊥BC,
∵OO′⊥平面ABC,BC?平面ABC,
∴OO′⊥BC,又AD⊥BC,AD?平面OAD,OO′?平面OAD,OO′∩AD=O′,
∴BC⊥平面OAD,∵OA?平面OAD,
∴BC⊥OA,
∵PS∥BC,OA∥SR,
∴PS⊥SR,
∴平行四边形PQRS是矩形.
故答案为:矩形.
点评 本题考查了线面平行的性质,线面垂直的判定与性质,属于中档题.

练习册系列答案
相关题目
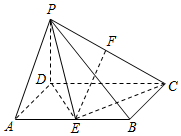 如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=2AD,PD⊥底面ABCD,E,F分别为棱AB,PC的中点.
如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=2AD,PD⊥底面ABCD,E,F分别为棱AB,PC的中点.