题目内容
已知数列{bn}的前n项和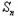 =
= n2﹣
n2﹣ n.数列{
n.数列{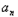 }满足(
}满足(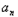 )3=4﹣(bn+2),n∈N*,数列{cn}满足cn=
)3=4﹣(bn+2),n∈N*,数列{cn}满足cn=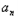 bn.
bn.
(1)求数列{cn}的前n项和Tn;
(2)若cn≤ m2+m﹣1对一切正整数n恒成立,求实数m的取值范围.
m2+m﹣1对一切正整数n恒成立,求实数m的取值范围.
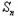 =
= n2﹣
n2﹣ n.数列{
n.数列{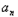 }满足(
}满足(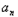 )3=4﹣(bn+2),n∈N*,数列{cn}满足cn=
)3=4﹣(bn+2),n∈N*,数列{cn}满足cn=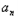 bn.
bn.(1)求数列{cn}的前n项和Tn;
(2)若cn≤
 m2+m﹣1对一切正整数n恒成立,求实数m的取值范围.
m2+m﹣1对一切正整数n恒成立,求实数m的取值范围.解:(1)由已知得,
当n≥2时,bn=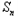 ﹣
﹣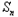 ﹣1=(
﹣1=( n2﹣
n2﹣ n)﹣[
n)﹣[ (n﹣1)2﹣
(n﹣1)2﹣ (n﹣1)]=3n﹣2
(n﹣1)]=3n﹣2
又b1=1=3×1﹣2,符合上式,
故数列{bn}的通项公式为bn=3n﹣2.
∵数列{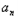 }满足(
}满足(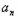 )3=4﹣(bn+2)
)3=4﹣(bn+2)
∴(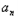 )3=4﹣3n,
)3=4﹣3n,
∴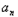 =4﹣n,
=4﹣n,
∴cn=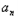 bn=(3n﹣2)×4﹣n,
bn=(3n﹣2)×4﹣n,
∴Tn=1×4﹣1+4×4﹣2+…+(3n﹣2)×4﹣n,①
∴ Tn=1×4﹣2+4×4﹣3+…+(3n﹣2)×4﹣n﹣1,②
Tn=1×4﹣2+4×4﹣3+…+(3n﹣2)×4﹣n﹣1,②
①﹣②得 Tn=4﹣1+3[4﹣2+4﹣3+…+4﹣n]﹣(3n﹣2)×4﹣n﹣1=
Tn=4﹣1+3[4﹣2+4﹣3+…+4﹣n]﹣(3n﹣2)×4﹣n﹣1= ﹣(3n﹣2)×4﹣n﹣1,
﹣(3n﹣2)×4﹣n﹣1,
∴Tn= ﹣
﹣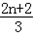 ×4﹣n;
×4﹣n;
(2)∵cn=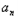 bn=(3n﹣2)×4﹣n,
bn=(3n﹣2)×4﹣n,
∴cn+1﹣cn=(3n+1)×4﹣n﹣1﹣(3n﹣2)×4﹣n=﹣9(n﹣1)×4﹣n﹣1,
当n=1时,cn+1=cn;
当n≥2时,cn+1<cn,
∴(cn)max=c1=c2=
若cn≤ m2+m﹣1对一切正整数n恒成立,则
m2+m﹣1对一切正整数n恒成立,则 m2+m﹣1≥
m2+m﹣1≥ 即可,
即可,
∴m2+4m﹣5≥0,
∴m≤﹣5或m≥1.
当n≥2时,bn=
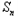 ﹣
﹣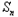 ﹣1=(
﹣1=( n2﹣
n2﹣ n)﹣[
n)﹣[ (n﹣1)2﹣
(n﹣1)2﹣ (n﹣1)]=3n﹣2
(n﹣1)]=3n﹣2又b1=1=3×1﹣2,符合上式,
故数列{bn}的通项公式为bn=3n﹣2.
∵数列{
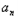 }满足(
}满足(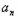 )3=4﹣(bn+2)
)3=4﹣(bn+2)∴(
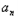 )3=4﹣3n,
)3=4﹣3n,∴
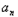 =4﹣n,
=4﹣n,∴cn=
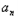 bn=(3n﹣2)×4﹣n,
bn=(3n﹣2)×4﹣n,∴Tn=1×4﹣1+4×4﹣2+…+(3n﹣2)×4﹣n,①
∴
 Tn=1×4﹣2+4×4﹣3+…+(3n﹣2)×4﹣n﹣1,②
Tn=1×4﹣2+4×4﹣3+…+(3n﹣2)×4﹣n﹣1,②①﹣②得
 Tn=4﹣1+3[4﹣2+4﹣3+…+4﹣n]﹣(3n﹣2)×4﹣n﹣1=
Tn=4﹣1+3[4﹣2+4﹣3+…+4﹣n]﹣(3n﹣2)×4﹣n﹣1= ﹣(3n﹣2)×4﹣n﹣1,
﹣(3n﹣2)×4﹣n﹣1,∴Tn=
 ﹣
﹣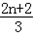 ×4﹣n;
×4﹣n; (2)∵cn=
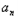 bn=(3n﹣2)×4﹣n,
bn=(3n﹣2)×4﹣n,∴cn+1﹣cn=(3n+1)×4﹣n﹣1﹣(3n﹣2)×4﹣n=﹣9(n﹣1)×4﹣n﹣1,
当n=1时,cn+1=cn;
当n≥2时,cn+1<cn,
∴(cn)max=c1=c2=

若cn≤
 m2+m﹣1对一切正整数n恒成立,则
m2+m﹣1对一切正整数n恒成立,则 m2+m﹣1≥
m2+m﹣1≥ 即可,
即可,∴m2+4m﹣5≥0,
∴m≤﹣5或m≥1.

练习册系列答案
相关题目