题目内容
9.已知函数f(x)=x+$\frac{a}{x}$,g(x)=-xe-x,若对任意的x1∈[1,e],存在x2∈[0,2],使得f(x1)≥g(x2),则a的取值范围为$[-1-\frac{1}{e},+∞)$.分析 对任意的x1∈[1,e],存在x2∈[0,2],使得f(x1)≥g(x2),等价于f(x1)min≥g(x2)min.g(x)=-xe-x,x∈[0,2],g′(x)=(x-1)e-x,可知x=1时函数g(x)取得极小值,g(1)=$-\frac{1}{e}$.x+$\frac{a}{x}$≥$-\frac{1}{e}$恒成立,x∈[1,e],化为:a≥-x2-$\frac{1}{e}x$=$-(x+\frac{1}{2e})^{2}$+$\frac{1}{4{e}^{2}}$=u(x),利用二次函数的单调性即可得出.
解答 解:对任意的x1∈[1,e],存在x2∈[0,2],使得f(x1)≥g(x2),
等价于f(x1)min≥g(x2)min.
g(x)=-xe-x,x∈[0,2],g′(x)=(x-1)e-x,可知x=1时函数g(x)取得极小值,g(1)=$-\frac{1}{e}$.
∴x+$\frac{a}{x}$≥$-\frac{1}{e}$恒成立,x∈[1,e],
化为:a≥-x2-$\frac{1}{e}x$=$-(x+\frac{1}{2e})^{2}$+$\frac{1}{4{e}^{2}}$=u(x),
u(x)在x∈[1,e]上单调递减,因此x=1时,u(x)取得最大值-1-$\frac{1}{e}$,
∴a≥-1-$\frac{1}{e}$,
∴a的取值范围为$[-1-\frac{1}{e},+∞)$.
故答案为:$[-1-\frac{1}{e},+∞)$.
点评 本题考查了利用导数研究函数的单调性极值与最值、不等式的性质、二次函数的单调性,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
14.已知点M(-1,0),N(1,0),若直线上存在点P,使得|PM|+|PN|=4,则称该直线为“A型直线”,给出下列直线:①y=x+3;②x=-2;③y=2;④y=2x+1,其中为“A类直线”的是( )
| A. | ①③ | B. | ②④ | C. | ②③ | D. | ③④ |
19.设凸k(k≥3且k∈N)边形的对角线的条数为f(k),则凸k+1边形的对角线的条数为f(k+1)=f(k)+( )
| A. | k-1 | B. | k | C. | k+1 | D. | k2 |
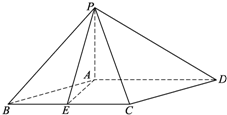 已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=2PA,E是线段BC的中点.
已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=2PA,E是线段BC的中点.