题目内容
18.形如y=$\frac{b}{|x|-c}$(c>0,b>0)的函数因其图象类似于汉字中的“囧”字,故我们把其生动地称为“囧函数”.若函数f(x)=loga(x2+x+1)(a>0,a≠1)有最小值,则当c,b的值分别为方程x2+y2-2x-2y+2=0中的x,y时的“囧函数”与函数y=loga|x|的图象交点个数为( )| A. | 1 | B. | 2 | C. | 4 | D. | 6 |
分析 由题意可得a>1,c=b=1,这时“囧函数”为$y=\frac{1}{|x|-1}$,它与函数y=loga|x|在同一坐标系内的图象如图所示,数形结合求得它们的图象交点个数.
解答 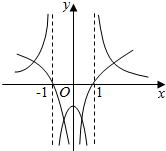 解:令u=x2+x+1,则$f(x)={log_a}({{x^2}+x+1})$是y=logau与u=x2+x+1复合函数,
解:令u=x2+x+1,则$f(x)={log_a}({{x^2}+x+1})$是y=logau与u=x2+x+1复合函数,
∵$u={(x+\frac{1}{2})^2}+\frac{3}{4}≥\frac{3}{4}$,当y=logau是增函数,$u∈[\frac{3}{4},+∞)$时有最小值,
所以,a>1;x2+y2-2x-2y+2=0,
即(x-1)2+(y-1)2=0,可得x=y=1,
所以,c=b=1,这时“囧函数”为$y=\frac{1}{|x|-1}$,
它与函数y=loga|x|在同一坐标系内的图象如图所示,
数形结合可得它们的图象交点个数为4,
故选:C.
点评 本题主要考查函数的图象特征,两个函数的图象交点个数,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.若某中学高二年级8个班参加合唱比赛的得分如茎叶图所示,则这组数据的中位数是( )


| A. | 91.5 | B. | 92.5 | C. | 91 | D. | 92 |
6.f(3x)=x,则f(10)=( )
| A. | log310 | B. | lg3 | C. | 103 | D. | 310 |
10.若x1,x2,x3,…,xn的平均数为$\overline x$,则x1+a,x2+a,…,xn+a的平均数为( )
| A. | $\overline x+a$ | B. | $a\overline x$ | C. | ${a^2}\overline x$ | D. | $\overline x+{a^2}$ |
7.若以F1(-3,0),F2(3,0)为焦点的双曲线与直线y=x-1有公共点,则该双曲线的离心率的最小值为( )
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\frac{3\sqrt{5}}{5}$ | C. | $\frac{3}{2}$ | D. | $\sqrt{3}$ |
8.已知α,β∈($\frac{7π}{4}$,$\frac{9π}{4}$),则“tan2α>tan2β”是“3α>3β”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |