题目内容
17.已知等比数列{an}中,各项都是正数,且3a1,$\frac{1}{2}$a3,2a2成等差数列,则等比数列{an}公比q等于( )| A. | 3 | B. | 9 | C. | 27 | D. | 81 |
分析 利用等比数列的通项公式及等差数列的性质列出方程组,由此能求出等比数列{an}公比q.
解答 解:∵等比数列{an}中,各项都是正数,且3a1,$\frac{1}{2}$a3,2a2成等差数列,
∴$\left\{\begin{array}{l}{q>0}\\{2[\frac{1}{2}{a}_{1}{q}^{2}]=3{a}_{1}+2{a}_{1}q}\end{array}\right.$,
即$\left\{\begin{array}{l}{q>0}\\{{q}^{2}-2q-3=0}\end{array}\right.$,解得q=3.
∴等比数列{an}公比q等于3.
故选:A.
点评 本题考查等比数列的公比的求法,是基础题,解题时要认真审题,注意等差数列、等比数列的性质的合理运用.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
7.计算 log3$\sqrt{27}$+lg25+lg4+7${\;}^{lo{g}_{7}2}$+(-9.8)0 值为( )
| A. | 6 | B. | 8 | C. | $\frac{10}{3}$ | D. | $\frac{13}{2}$ |
5.直线${l_1}:x+{a^2}y+6=0$和直线l2:(a-2)x+3ay+2a=0.若l1∥l2,则a的值为( )
| A. | -1 | B. | 0 | C. | 0或-1 | D. | 0或1 |
12.如图所示的程序框图中,输出的B是( )
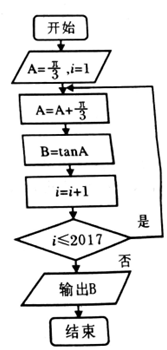

| A. | $\sqrt{3}$ | B. | 0 | C. | -$\frac{\sqrt{3}}{3}$ | D. | -$\sqrt{3}$ |
6.从装有2个红球和2个黑球的口袋内任取2个球,则与事件恰有两个红球既不对立也不互斥的事件是( )
| A. | 至少有一个黑球 | B. | 恰好一个黑球 | C. | 至多有一个红球 | D. | 至少有一个红球 |