题目内容
6.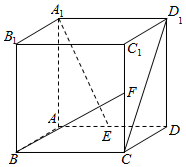 如图,设正方形ABCD-A1B1C1D1的棱长为2,E、F分别是AD和CC1的中点.
如图,设正方形ABCD-A1B1C1D1的棱长为2,E、F分别是AD和CC1的中点.(1)求证:A1E⊥BF;
(2)求异面直线A1E与CD1所成角的余弦值.
分析 (1)以A为原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,利用向量法能证明A1E⊥BF.
(2)求出$\overrightarrow{{A}_{1}E}$,$\overrightarrow{C{D}_{1}}$,利用向量法能求出异面直线A1E与CD1所成角的余弦值.
解答 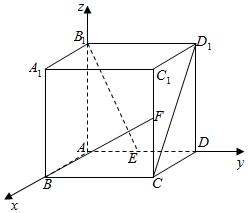 证明:(1以A为原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,
证明:(1以A为原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,
∵正方形ABCD-A1B1C1D1的棱长为2,E、F分别是AD和CC1的中点,
∴A1(0,0,2),E(0,1,0),B(2,0,0),F(2,2,1),
$\overrightarrow{{A}_{1}E}$=(0,1,-2),$\overrightarrow{BF}$=(0,2,1),
$\overrightarrow{{A}_{1}E}$•$\overrightarrow{BF}$=0+2-2=0,
∴A1E⊥BF.
解:(2)$\overrightarrow{{A}_{1}E}$=(0,1,-2),C(2,2,0),D1(0,2,2),
$\overrightarrow{C{D}_{1}}$=(-2,0,2),
设异面直线A1E与CD1所成角为θ,
cosθ=|$\frac{\overrightarrow{{A}_{1}E}•\overrightarrow{C{D}_{1}}}{|\overrightarrow{{A}_{1}E}|•|\overrightarrow{C{D}_{1}}|}$|=$\frac{4}{\sqrt{5}•\sqrt{8}}$=$\frac{\sqrt{10}}{5}$.
∴异面直线A1E与CD1所成角的余弦值为$\frac{\sqrt{10}}{5}$.
点评 本考查异面直线垂直的证明,考查异面直线所成角的余弦值的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

 阅读快车系列答案
阅读快车系列答案| A. | 30° | B. | 60° | C. | 90° | D. | 45° |
①若一个平面内的两条直线都与另一个平面平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③一条直线垂直于一个平面内的无数条直线,则这条直线和这个平面垂直;
④垂直于同一直线的两平面互相平行.
| A. | ①和② | B. | ②和③ | C. | ②和④ | D. | ③和④ |
 已知抛物线y2=2px(p>0)的焦点为F,点P是抛物线上横坐标为3的点,且P到抛物线焦点F的距离等于4.
已知抛物线y2=2px(p>0)的焦点为F,点P是抛物线上横坐标为3的点,且P到抛物线焦点F的距离等于4.