题目内容
曲线y=ex+x在点(0,1)处的切线方程为 .
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:欲求在点(0,1)处的切线的方程,只须求出其斜率即可,故先利用导数求出在x=0处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.
解答:
解:∵y=ex+x,
∴y′=ex+1,
∴曲线y=ex+x在点(0,1)处的切线的斜率为:k=2,
∴曲线y=ex+x在点(0,1)处的切线的方程为:y-1=2x,即y=2x+1.
故答案为:y=2x+1.
∴y′=ex+1,
∴曲线y=ex+x在点(0,1)处的切线的斜率为:k=2,
∴曲线y=ex+x在点(0,1)处的切线的方程为:y-1=2x,即y=2x+1.
故答案为:y=2x+1.
点评:本题考查利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
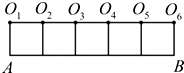 如图,在5个并排的正方形图案中作出一个∠AOnB=135°(n=1,2,3,4,5,6),则n=( )
如图,在5个并排的正方形图案中作出一个∠AOnB=135°(n=1,2,3,4,5,6),则n=( )| A、1,6 | B、2,5 |
| C、3,4 | D、2,3,4,5 |
已知M是椭圆
+
=1上在第一象限的点,点A和点B分别是椭圆的右顶点和上顶点,O为原点,求四边形MAOB的面积的最大值( )
| x2 |
| 25 |
| y2 |
| 16 |
| A、10 | ||
B、10
| ||
| C、200 | ||
D、200
|
已知数列{an}的前n项的是Sn=n2,则a6的值是( )
| A、9 | B、10 | C、11 | D、12 |