题目内容
设命题p：函数f（x）=
在（0，+∞）上是增函数；命题q：方程x2+
x+b-2=0有两个不相等的负实数根，若p∧q是真命题．
（1）求点P（a，b）的轨迹图形的面积；
（2）求a+5b的取值范围．
| (a+5)x+b |
| x+1 |
| -a |
（1）求点P（a，b）的轨迹图形的面积；
（2）求a+5b的取值范围．
考点：简单线性规划,利用导数研究函数的单调性,基本不等式
专题：不等式的解法及应用
分析：（1）根据复合命题之间的关系建立条件关系，作出对应的图象即可求点P（a，b）的轨迹图形的面积；
（2）利用线性规划的知识即可求a+5b的取值范围．
（2）利用线性规划的知识即可求a+5b的取值范围．
解答：
解：（1）∵f（x）=
，f′（x）=
，
∴p真?x∈（0，+∞）时，
＞0?a-b+5＞0，（2′）
∵方程x2+
x+b-2=0有两个不相等的负实数根?
?
，即q真?
；
若p∧q是真命题．则p真q真，∴
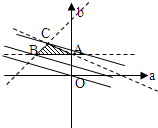
点P（a，b）的轨迹图形如图，△ABC 的内部；
由边界可得A（0，2），B（-3，2），C（-
，
）
∴△ABC的面积S=
×3×（
-2）=
，即点P（a，b）的轨迹图形的面积为
；
（2）设a+5b=z，直线a+5b=z过B点时，z=-3+5×2=7，直线a+5b=z过C点时，
z=-
+5×
=
，
∴a+5b的取值范围是（7，
）
解：（1）∵f（x）=| (a+5)x+b |
| x+1 |
| a+5-b |
| (x+1)2 |
∴p真?x∈（0，+∞）时，
| a+5-b |
| (x+1)2 |
∵方程x2+
| -a |
|
|
|
若p∧q是真命题．则p真q真，∴
|
由边界可得A（0，2），B（-3，2），C（-
| 12 |
| 5 |
| 13 |
| 5 |
∴△ABC的面积S=
| 1 |
| 2 |
| 13 |
| 5 |
| 9 |
| 10 |
| 9 |
| 10 |
（2）设a+5b=z，直线a+5b=z过B点时，z=-3+5×2=7，直线a+5b=z过C点时，
z=-
| 12 |
| 5 |
| 13 |
| 5 |
| 53 |
| 5 |
∴a+5b的取值范围是（7，
| 53 |
| 5 |
点评：本题主要考查线性规划的应用，利用数形结合是解决本题的关键．综合性较强．
练习册系列答案
相关题目
设集合A={1，2}，B={2，3，4}，则A∩B=（ ）
| A、{1，2，3，4} |
| B、{1，2，2，3，4} |
| C、{2} |
| D、{1，3，4} |
函数y=log
（x2-6x+8）的单调递增区间是（ ）
| 1 |
| 3 |
| A、（3，+∞） |
| B、（-∞，3） |
| C、（4，+∞） |
| D、（-∞，2） |