题目内容
14.已知y=$\sqrt{2x-{x}^{2}}$,那么$\frac{y}{x+1}$的取值范围是$[0,\frac{\sqrt{3}}{3}]$.分析 由2x-x2≥0,解得0≤x≤2.y=$\sqrt{2x-{x}^{2}}$的定义域为[0,2].两边平方可得:(x-1)2+y2=1.画出图象:则$\frac{y}{x+1}$表示半圆上的点(x,y)与(-1,0)连线的斜率.再利用直线与圆相切的性质即可得出.
解答 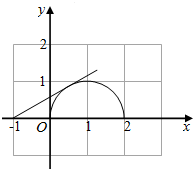 解:由2x-x2≥0,解得0≤x≤2.
解:由2x-x2≥0,解得0≤x≤2.
∴y=$\sqrt{2x-{x}^{2}}$的定义域为[0,2].
两边平方可得:(x-1)2+y2=1.
画出图象:
则$\frac{y}{x+1}$表示半圆上的点(x,y)与(-1,0)连线的斜率.
当经过点(-1,0)的直线y=k(x+1)(k>0)与圆相切时,可得$\frac{|k-0+k|}{\sqrt{1+{k}^{2}}}$=1,解得k=$\frac{\sqrt{3}}{3}$.
那么$\frac{y}{x+1}$的取值范围是$[0,\frac{\sqrt{3}}{3}]$.
故答案为:$[0,\frac{\sqrt{3}}{3}]$.
点评 本题考查了直线与圆相切性质、点到直线的距离公式、斜率计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.已知函数f(x)=ax2+bx+1具有以下性质:
①对任意实数x1≠x2,且f(x1)=f(x2)时,满足x1+x2=2.
②对任意x1,x2∈(1,+∞)上,总有f($\frac{{x}_{1}+{x}_{2}}{2}$)>$\frac{f({x}_{1})+f({x}_{2})}{2}$.
则方程ax2+bx+1=0根的情况是( )
①对任意实数x1≠x2,且f(x1)=f(x2)时,满足x1+x2=2.
②对任意x1,x2∈(1,+∞)上,总有f($\frac{{x}_{1}+{x}_{2}}{2}$)>$\frac{f({x}_{1})+f({x}_{2})}{2}$.
则方程ax2+bx+1=0根的情况是( )
| A. | 无实数根 | B. | 有两个不等正根 | C. | 有两个异号实根 | D. | 有两个相等正根 |
14.已知函数f(x)在(0,$\frac{π}{2}$)上处处可导,若[f(x)-f′(x)]tanx-f(x)<0,则( )
| A. | $f(ln\frac{3}{2})sin(ln\frac{3}{2})$一定小于$0.6f(ln\frac{5}{2})sin(ln\frac{5}{2})$ | |
| B. | $f(ln\frac{3}{2})sin(ln\frac{3}{2})$一定大于$0.6f(ln\frac{5}{2})sin(ln\frac{5}{2})$ | |
| C. | $f(ln\frac{3}{2})sin(ln\frac{3}{2})$可能大于$0.6f(ln\frac{5}{2})sin(ln\frac{5}{2})$ | |
| D. | $f(ln\frac{3}{2})sin(ln\frac{3}{2})$可能等于$0.6f(ln\frac{5}{2})sin(ln\frac{5}{2})$ |