题目内容
甲、乙、丙3人站到共有7级的台阶上,若每级台阶最多站3 人,同一级台阶上的人不区分站的位置,则不同的站法种数是 (用数字作答).
考点:计数原理的应用
专题:计算题,排列组合
分析:根据题意,分析可得甲、乙、丙3人都有7种不同的站法,由分步计数原理计算可得答案.
解答:
解:根据题意,甲、乙、丙3人站到共有7级的台阶上,
则甲有7种选择,即甲有7种站法,
同理乙、丙2人也有7种站法,
则甲、乙、丙3人共有7×7×7=343种不同的站法;
故答案为343.
则甲有7种选择,即甲有7种站法,
同理乙、丙2人也有7种站法,
则甲、乙、丙3人共有7×7×7=343种不同的站法;
故答案为343.
点评:本题考查分步计数原理的应用,注意本题中“若每级台阶最多站3 人,同一级台阶上的人不区分站的位置”的条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
执行如图所示的程序框图,输出的k值为( )


| A、3 | B、4 | C、5 | D、6 |
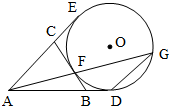 如图,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G,给出下列三个结论:①AD+AE=AB+BC+CA,②AF•AG=AD•AE,③△AFB∽△ADG,其中正确结论的序号是
如图,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G,给出下列三个结论:①AD+AE=AB+BC+CA,②AF•AG=AD•AE,③△AFB∽△ADG,其中正确结论的序号是设平面上有四个相异的点A、B、C、D,已知(
+
-2
)•(
-
)=0,则△ABC的形状是( )
| DB |
| DC |
| DA |
| DB |
| DC |
| A、直角三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
 在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°,设AA1=a.
在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°,设AA1=a.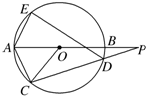 如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,AE=AC,求证:∠PDE=∠POC.
如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,AE=AC,求证:∠PDE=∠POC. 四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD,PD=AD=1,则点B到平面PAC的距离为
四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD,PD=AD=1,则点B到平面PAC的距离为 如图,矩形ABEF和正方形ABCD有公共边AB,它们所在平面成60°的二面角,AB=CB=2a,BE=a,则DE=
如图,矩形ABEF和正方形ABCD有公共边AB,它们所在平面成60°的二面角,AB=CB=2a,BE=a,则DE=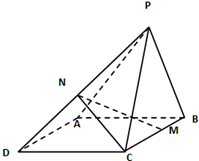 如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠ABC=60°,AB=2,△PCB为正三角形,且平面PCB⊥平面ABCD,M,N分别为BC,PD的中点.
如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠ABC=60°,AB=2,△PCB为正三角形,且平面PCB⊥平面ABCD,M,N分别为BC,PD的中点.