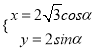题目内容
【题目】已知圆![]() 的圆心为原点
的圆心为原点![]() ,且与直线
,且与直线![]() 相切.
相切.
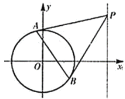
(1)求圆![]() 的方程;
的方程;
(2)点![]() 在直线
在直线![]() 上,过
上,过![]() 点引圆
点引圆![]() 的两条切线
的两条切线![]() ,
,![]() ,切点为
,切点为![]() ,
,![]() ,求证:直线
,求证:直线![]() 恒过定点.
恒过定点.
(3)求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)证明见解析(3)
(2)证明见解析(3)![]()
【解析】
![]() 根据题意,设圆C的半径为r,由直线与圆的位置关系可得
根据题意,设圆C的半径为r,由直线与圆的位置关系可得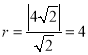 ,即可得圆的标准方程;
,即可得圆的标准方程;![]() 设
设![]() ,求出
,求出![]() 的值,求出以P为圆心,PA为半径为圆的方程,分析可得直线AB为圆C与圆P的公共弦所在的直线,联立2个圆的方程,即可得直线AB的方程,分析可得结论;
的值,求出以P为圆心,PA为半径为圆的方程,分析可得直线AB为圆C与圆P的公共弦所在的直线,联立2个圆的方程,即可得直线AB的方程,分析可得结论;![]() 根据题意,设
根据题意,设![]() ,
,![]() ,在
,在![]() 中,可得
中,可得![]() ,由数量积的计算公式可得
,由数量积的计算公式可得![]() ,结合b的范围分析可得答案.
,结合b的范围分析可得答案.
(1)由题知圆的半径![]()
∴圆![]() 的方程为
的方程为![]()
(2)设点![]() 则
则![]() ,
,
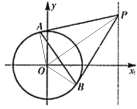
∴![]()
∴圆![]() 的方程为:
的方程为:![]() ①
①
又圆![]() 方程为:
方程为:![]() ②
②
由①—②得![]() 即为
即为![]()
∴直线![]() 方程为:
方程为:![]()
∴直线![]() 过定点
过定点![]()
(3)设![]() ,则
,则![]()
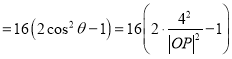
![]()
∴![]() 的取值范围是
的取值范围是![]()

练习册系列答案
相关题目