题目内容
18．下列函数中，在（0，+∞）上单调递增的函数是（ ）| A． | f（x）=$\frac{1}{x}$ | B． | f（x）=sinx | C． | f（x）=cosx | D． | f（x）=x${\;}^{\frac{1}{2}}$ |
分析 根据反比例函数和正余弦函数的单调性便可判断前三项错误，而根据增函数的定义和f（x）=${x}^{\frac{1}{2}}$的图象便可判断选项D正确．
解答 解：A.$f（x）=\frac{1}{x}$在（0，+∞）上单调递减，∴该选项错误；
B．f（x）=sinx在（0，+∞）上没有单调性，∴该选项错误；
C．f（x）=cosx在（0，+∞）上没有单调性，∴该选项错误；
D.$f（x）={x}^{\frac{1}{2}}$在（0，+∞）上单调递增，∴该选项正确．
故选：D．
点评 考查反比例函数的单调性，正弦函数和余弦函数的单调性，以及单调性的定义，要清楚$f（x）={x}^{\frac{1}{2}}$的图象．
练习册系列答案
相关题目
的展开式中，含
项的二项式系数为 ；系数为 ．（均用数字作答）
6．在等腰三角形ABC中，过直角顶点C在∠ACB内作一条射线CD与线段AB交于点D，则AD＜AC的概率是（ ）
| A． | $\frac{{\sqrt{2}}}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{{2-\sqrt{2}}}{2}$ | D． | $\frac{3}{4}$ |
13．函数f（x）=lgx-sinx在（0，+∞）的零点个数是（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
7．
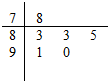对某同学的6次数学测试成绩（满分100分）进行统计，作出的茎叶如图所示，给出关于该同学数学成绩的以下说法：
①中位数为83；②众数为83；③平均数为85；④极差为12．
其中正确说法序号是（ ）
对某同学的6次数学测试成绩（满分100分）进行统计，作出的茎叶如图所示，给出关于该同学数学成绩的以下说法：①中位数为83；②众数为83；③平均数为85；④极差为12．
其中正确说法序号是（ ）
| A． | ①② | B． | ③④ | C． | ②③ | D． | ①③ |
8．已知离心率为e的椭圆Γ：$\frac{{x}^{2}}{{a}^{2}-4}$+$\frac{{y}^{2}}{{a}^{2}}$=1（a＞2）的上、下焦点分别为F1和F2，过点（0，2）且不与y轴垂直的直线与椭圆交于M，N两点，若△MNF2为等腰直角三角形，则e=（ ）
| A． | $\sqrt{3}$-$\sqrt{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\sqrt{6}$$-\sqrt{3}$ | D． | $\frac{\sqrt{6}}{3}$ |