题目内容
9.已知集合A={x|2x>8},B={x|x2-3x-4<0}.(1)求A,B;
(2)设全集U=R,求(∁UA)∩B.
分析 (1)根据指数函数的图象与性质,求出集合A,再解一元二次不等式求出集合B;
(2)根据补集与交集的定义,求出(∁UA)∩B.
解答 解:(1)∵2x>8=23,且函数y=2x在R上是单调递增,
∴x>3,
∴A=(3,+∞);
又x2-3x-4<0可化为(x-4)(x+1)<0,
解得-1<x<4,
∴B=(-1,4);
(2)∵全集U=R,A=(3,+∞),
∴∁UA=(-∞,3];
又B=(-1,4),
∴(∁UA)∩B=(-1,3].
点评 本题考查了不等式的解法与应用问题,也考查了集合的化简与运算问题,是基础题目.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
1.已知全集I={0,1,2,3,4},集合A={1,2},B={2,3,4},则A∪(∁IB)=( )
| A. | {1} | B. | {2,3} | C. | {0,1,2} | D. | {0,2,3} |
18.下列函数中,在(0,+∞)上单调递增的函数是( )
| A. | f(x)=$\frac{1}{x}$ | B. | f(x)=sinx | C. | f(x)=cosx | D. | f(x)=x${\;}^{\frac{1}{2}}$ |
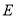 的方程为
的方程为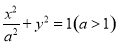 ,
,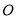 为坐标原点,直线
为坐标原点,直线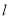 与椭圆
与椭圆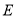 交于点
交于点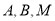 为线段
为线段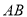 的中点.
的中点.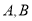 分别为
分别为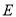 的左顶点和上顶点,且
的左顶点和上顶点,且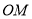 的斜率为
的斜率为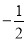 ,求
,求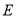 的标准方程;
的标准方程;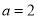 ,且
,且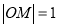 ,求
,求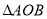 面积的最大值.
面积的最大值.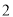 的等边
的等边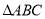 的边角地,现修成草坪,图中
的边角地,现修成草坪,图中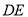 把草坪分成面积相等的两部分,
把草坪分成面积相等的两部分, 在
在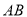 上,
上,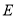 在
在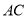 上.
上.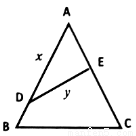
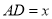 (
(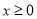 ),
), ,求用
,求用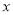 表示
表示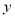 的函数关系式;
的函数关系式;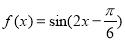 的图象,可以将函数
的图象,可以将函数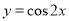 的图象( )
的图象( )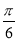 个单位长度
个单位长度 个单位长度
个单位长度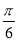 个单位长度
个单位长度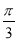 个单位长度
个单位长度