题目内容
设函数f(x)=lnx-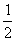 ax2-bx.
ax2-bx.
(1)当a=b=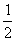 时,求f(x)的最大值.
时,求f(x)的最大值.
(2)令F(x)=f(x)+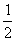 ax2+bx+
ax2+bx+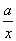 (0<x≤3),其图像上任意一点P(x0,y0)处的切线的斜率k≤
(0<x≤3),其图像上任意一点P(x0,y0)处的切线的斜率k≤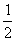 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
解:(1)依题意,知f(x)的定义域为(0,+∞).
当a=b= 时,f(x)=lnx-
时,f(x)=lnx- x2-
x2- x,
x,
f'(x)= -
- x-
x- =
= ,
,
令f'(x)=0,解得x=1或x=-2(舍去).
当0<x<1时,f'(x)>0,f(x)是增加的;
当x>1时,f'(x)<0,f(x)是减少的.
所以f(x)的极大值为f(1)=- ,
,
即f(x)的最大值是- .
.
(2)F(x)=lnx+ ,x∈(0,3],
,x∈(0,3],
则有k=F'(x0)= ≤
≤ 在(0,3]上恒成立,
在(0,3]上恒成立,
所以a≥(- +x0)max,
+x0)max,
当x0=1时,- +x0取得最大值
+x0取得最大值 ,所以a≥
,所以a≥ .
.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
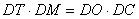 ;(Ⅱ)若
;(Ⅱ)若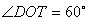 ,试求
,试求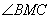 的大小.
的大小.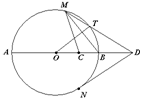
 的值为__ ___.
的值为__ ___.
 }(n∈N*)的前n项和为( )
}(n∈N*)的前n项和为( ) (B)
(B) (C)
(C) (D)
(D)
 ;
; 的定义域为________.
的定义域为________.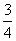 ,且2
,且2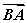 ·
·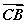 =-27.
=-27.