题目内容
若函数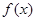 在定义域内存在区间
在定义域内存在区间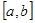 ,满足
,满足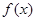 在
在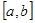 上的值域为
上的值域为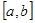 ,则称这样的函数
,则称这样的函数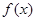 为“优美函数”.
为“优美函数”.
(Ⅰ)判断函数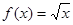 是否为“优美函数”?若是,求出
是否为“优美函数”?若是,求出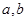 ;若不是,说明理由;
;若不是,说明理由;
(Ⅱ)若函数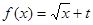 为“优美函数”,求实数
为“优美函数”,求实数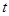 的取值范围.
的取值范围.
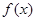 在定义域内存在区间
在定义域内存在区间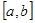 ,满足
,满足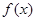 在
在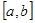 上的值域为
上的值域为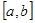 ,则称这样的函数
,则称这样的函数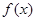 为“优美函数”.
为“优美函数”.(Ⅰ)判断函数
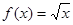 是否为“优美函数”?若是,求出
是否为“优美函数”?若是,求出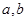 ;若不是,说明理由;
;若不是,说明理由;(Ⅱ)若函数
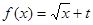 为“优美函数”,求实数
为“优美函数”,求实数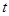 的取值范围.
的取值范围.(I) (II)
(II)
 (II)
(II)
第一问中,利用定义,判定由题意得 ,由
,由 ,所以
,所以
第二问中, 由题意得方程 有两实根
有两实根
设 所以关于m的方程
所以关于m的方程 在
在 有两实根,
有两实根,
即函数 与函数
与函数 的图像在
的图像在 上有两个不同交点,从而得到t的范围。
上有两个不同交点,从而得到t的范围。
解(I)由题意得 ,由
,由 ,所以
,所以 (6分)
(6分)
(II)由题意得方程 有两实根
有两实根
设 所以关于m的方程
所以关于m的方程 在
在 有两实根,
有两实根,
即函数 与函数
与函数 的图像在
的图像在 上有两个不同交点。
上有两个不同交点。

 ,由
,由 ,所以
,所以
第二问中, 由题意得方程
 有两实根
有两实根设
 所以关于m的方程
所以关于m的方程 在
在 有两实根,
有两实根,即函数
 与函数
与函数 的图像在
的图像在 上有两个不同交点,从而得到t的范围。
上有两个不同交点,从而得到t的范围。解(I)由题意得
 ,由
,由 ,所以
,所以 (6分)
(6分)(II)由题意得方程
 有两实根
有两实根设
 所以关于m的方程
所以关于m的方程 在
在 有两实根,
有两实根,即函数
 与函数
与函数 的图像在
的图像在 上有两个不同交点。
上有两个不同交点。

练习册系列答案
相关题目
 ,若
,若 在点
在点 处的切线斜率为
处的切线斜率为 .
. 表示
表示 ;
; ,若
,若 对定义域内的
对定义域内的 恒成立,
恒成立, ,证明:
,证明: .
. 是函数
是函数 的极值点.
的极值点. 时,求函数
时,求函数 的单调区间;
的单调区间; R时,函数
R时,函数
 有两个零点,求实数m的取值范围.
有两个零点,求实数m的取值范围. ,若存在区间
,若存在区间 ,使得
,使得 ,则称区间
,则称区间 为函数
为函数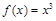 ; ②
; ②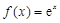 ; ③
; ③ .
. 在[-1,2]上的最大值为4,最小值为m,且函数
在[-1,2]上的最大值为4,最小值为m,且函数 在
在 上是增函数,则a=____.
上是增函数,则a=____. 米,宽
米,宽 米的长方形体育馆.按照建筑要求,每隔
米的长方形体育馆.按照建筑要求,每隔 米(
米( ,
,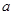 为正常数)需打建一个桩位,每个桩位需花费
为正常数)需打建一个桩位,每个桩位需花费 万元(桩位视为一点且打在长方形的边上),桩位之间的
万元(桩位视为一点且打在长方形的边上),桩位之间的 万元,在不计地板和天花板的情况下,当
万元,在不计地板和天花板的情况下,当 是定义在正整数集上的函数,且
是定义在正整数集上的函数,且 成立时,总可推出
成立时,总可推出 成立”,那么,下列命题总成立的是( )
成立”,那么,下列命题总成立的是( ) 成立,则
成立,则 成立
成立 成立,则当
成立,则当 时,均有
时,均有
 成立,则
成立,则 成立
成立  成立,则当
成立,则当 时,均有
时,均有 ,若
,若 ,则
,则



