题目内容
15.已知f(x)=ax3+bx2+c的图象经过点(0,1),且在x=1处的切线方程是y=x(1)求y=f(x)的解析式;
(2)求y=f(x)的极值.
分析 (1)求出c的值,求出函数的导数,计算f′(1),得到关于a,b的方程组,求出函数的解析式即可;
(2)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值即可.
解答 解:(1)f(x)=ax3+bx2+c的图象经过点(0,1),则c=1,…(2分)
f′(x)=3ax2+2bx,k=f′(1)=3a+2b=1…(3分)
切点为(1,1),则f(x)=ax3+bx2+c的图象经过点(1,1)
得a+b+c=1,得a=1,b=-1…(5分),
故f(x)=x3-x2+1…(6分)
(2)${f^'}(x)=3{x^2}-2x>0,得x>\frac{2}{3},x<0$,
令${f^'}(x)=3{x^2}-2x<0,得0<x<\frac{2}{3}$…(8分)
函数f(x)在$({-∞,0}),({\frac{2}{3},+∞})$单调递增,在$({0,\frac{2}{3}})$单调递减 …(9分)
所以函数f(x)在x=0取得极大值为1,在$x=\frac{2}{3}$取得极小值为$\frac{23}{27}$.
点评 本题考查了函数的单调性、极值问题,考查导数的应用,是一道中档题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
3.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1、F2,过F2的直线与椭圆交于A、B两点,若△F1AB是等边三角形,则离心率为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{3}{4}$ |
10.函数f(x),x∈R满足如下性质:①f(x)+f(-x)=0;②f($\frac{3}{4}$+x)=f($\frac{3}{4}$-x),若f(1)=-$\frac{\sqrt{5}}{5}$,f(2)=sinα(α∈(0,$\frac{π}{2}$)),则sin($\frac{π}{4}$+α)=( )
| A. | 0 | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{2\sqrt{10}}{10}$ | D. | $\frac{3\sqrt{10}}{10}$ |
20.若两点的坐标是A(3cosα,3sinα,1),B(2cosβ,2sinβ,1),则|AB|的取值范围是( )
| A. | [0,5] | B. | [1,5] | C. | (0,5) | D. | [1,25] |
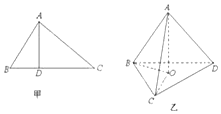 如图甲,在△ABC中,AB⊥AC,AD⊥BC,D为.垂足,则AB2=BD•BC,该结论称为射影定理.如图乙,在三棱锥A-BCD中,AD⊥平面ABC,AO⊥平面BCD,O为垂足,且O在△BCD内,类比射影定理,探究S△ABC、S△BCO、S△BCD这三者之间满足的关是S△ABC2=S△BCO•S△BCD.
如图甲,在△ABC中,AB⊥AC,AD⊥BC,D为.垂足,则AB2=BD•BC,该结论称为射影定理.如图乙,在三棱锥A-BCD中,AD⊥平面ABC,AO⊥平面BCD,O为垂足,且O在△BCD内,类比射影定理,探究S△ABC、S△BCO、S△BCD这三者之间满足的关是S△ABC2=S△BCO•S△BCD.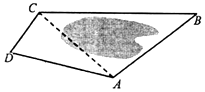 如图为了测量A,C两点间的距离,选取同一平面上B,D两点,测出四边形ABCD的各边的AB=5,BC=8,CD=3,DA=5长度(单位:km):,如图所示,若A、B、C、D四点共圆.
如图为了测量A,C两点间的距离,选取同一平面上B,D两点,测出四边形ABCD的各边的AB=5,BC=8,CD=3,DA=5长度(单位:km):,如图所示,若A、B、C、D四点共圆.