题目内容
20．求下列满足条件的圆的方程（1）圆心为C（2，-2）且过点P（6，3）的圆的方程
（2）己知点A（-4，-5），B（6，-1），求以线段AB为直径的圆的方程．
分析 （1）利用两点间的距离公式求出半径，根据圆心坐标写出圆的标准方程；
（2）由条件求出圆心坐标和圆的半径，即可得到圆的标准方程．
解答 解：（1）半径等于$\sqrt{（6-2）^{2}+（3+2）^{2}}$=$\sqrt{41}$，故圆的方程为 （x-2）2+（y+2）2=41；
（2）由中点坐标公式得线段AB的中点坐标为C（1，-3），
即圆心的坐标，r=$\sqrt{（1+4）^{2}+（-3+5）^{2}}$=$\sqrt{29}$，
故圆的方程为（x-1）2+（y+3）2=29．
点评 本题考查两点间的距离公式，求圆的方程的方法，求出圆心坐标和圆的半径是解题的关键，属于中档题．
练习册系列答案
名师点拨卷系列答案
相关题目
10．已知数列{an}满足an-an+1=an+1an（n∈N*），数列{bn}满足${b_n}=\frac{1}{a_n}$，且b1+b2+…+b10=65，则an=$\frac{1}{n+1}$．
11．
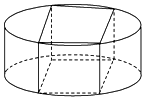将一个底面圆的直径为2、高为1的圆柱截成一个长方体，如图所示，设这个长方体底面的一条边长为x、对角线长为2，底面的面积为A．
（1）求面积A以x为自变量的函数式；
（2）求截得长方体的体积的最大值．
将一个底面圆的直径为2、高为1的圆柱截成一个长方体，如图所示，设这个长方体底面的一条边长为x、对角线长为2，底面的面积为A．（1）求面积A以x为自变量的函数式；
（2）求截得长方体的体积的最大值．
15．已知命题p：?x∈R，x2+x+1＜0，下列说法错误的是（ ）
| A． | 若￢p：?x∈R，x2+x+1≥0 | B． | p为假命题 | ||
| C． | p∨￢p为假命题 | D． | ￢p为真命题 |