题目内容
11.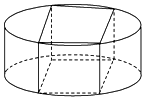 将一个底面圆的直径为2、高为1的圆柱截成一个长方体,如图所示,设这个长方体底面的一条边长为x、对角线长为2,底面的面积为A.
将一个底面圆的直径为2、高为1的圆柱截成一个长方体,如图所示,设这个长方体底面的一条边长为x、对角线长为2,底面的面积为A.(1)求面积A以x为自变量的函数式;
(2)求截得长方体的体积的最大值.
分析 (1)作出横截面,由这个长方体底面的一条边长为x、对角线长为2,能求出底面的面积A.
(2)长方体的体积V=x•$\sqrt{4-{x}^{2}}$•1,由此利用配方法能求出截得长方体的体积的最大值.
解答 解:(1)将一个底面圆的直径为2、高为1的圆柱截成一个长方体,
横截面如图,
设这个长方体底面的一条边长为x、对角线长为2,底面的面积为A.
由题意得A=x•$\sqrt{4-{x}^{2}}$(0<x<2).…(4分) (未写x的范围扣1分)
(未写x的范围扣1分)
(2)长方体的体积V=x•$\sqrt{4-{x}^{2}}$•1=$\sqrt{-({x}^{2}-2)^{2}+4}$,…(5分)
由(1)知0<x<2,
∴当x2=2,即x=$\sqrt{2}$时,Vmax=2. …(7分)
故截得长方体的体积的最大值为2. …(8分)
点评 本题考查长方体的底面面积的求法,考查长方体的体积的最大值的求法,考查推理论证能力、运算求解能力、空间思维能力,考查转化化归思想、数形结合思想,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.以下三个命题中,真命题的个数有( )个
①若$\frac{1}{a}$<$\frac{1}{b}$,则a<b;②若a>b>c,则a|c|>b|c|;③函数f(x)=x+$\frac{1}{x}$有最小值2.
①若$\frac{1}{a}$<$\frac{1}{b}$,则a<b;②若a>b>c,则a|c|>b|c|;③函数f(x)=x+$\frac{1}{x}$有最小值2.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
6.已知边长为1的正方形ABCD位于第一象限,且顶点A,D分别在x,y的正半轴上(含原点O)滑动,则|$\overrightarrow{OB}$+$\overrightarrow{OC}$|的最大值是( )
| A. | 1 | B. | 2 | C. | 3 | D. | $\sqrt{10}$ |
3.若集合A={-1,0,1,2,3},B={x|x2-2x-3<0},则A∩B等于( )
| A. | {-1,0} | B. | {-1,0,1,2} | C. | {0,1,2,3} | D. | {0,1,2} |
5.若存在实数a,b,对任意实数x∈[0,4],使不等式$\sqrt{x}$-m≤ax+b≤$\sqrt{x}$+m恒成立,则m的取值范围为( )
| A. | m≥1 | B. | m≤1 | C. | m≤$\frac{1}{4}$ | D. | m≥$\frac{1}{4}$ |
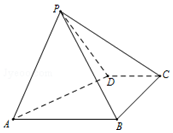 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,∠ABC=90°,AB∥CD,AB=AD=2,CD=1,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,∠ABC=90°,AB∥CD,AB=AD=2,CD=1,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形