题目内容
如图,在三棱锥 中,点
中,点 分别是棱
分别是棱 的中点.
的中点.
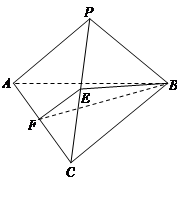
(1)求证: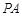 //平面
//平面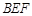 ;
;
(2)若平面 平面
平面 ,
,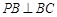 ,求证:
,求证: .
.
 中,点
中,点 分别是棱
分别是棱 的中点.
的中点.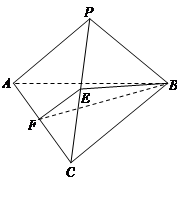
(1)求证:
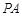 //平面
//平面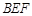 ;
;(2)若平面
 平面
平面 ,
,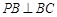 ,求证:
,求证: .
.(1)详见解析;(2)详见解析.
试题分析:(1)这是一个证明直线和平面平行的问题,考虑直线与平面平行的判定定理,可找面外线平行于面内线,本题容易找到
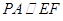 ,结论自然得证;(2)因为条件中有平面与平面垂直,故可考虑平面与平面垂直的判定定理,在一平面内作垂直于交线的直线平行于另一平面,再得到线线垂直,再证线面垂直,再得线线垂直,问题不难解决.
,结论自然得证;(2)因为条件中有平面与平面垂直,故可考虑平面与平面垂直的判定定理,在一平面内作垂直于交线的直线平行于另一平面,再得到线线垂直,再证线面垂直,再得线线垂直,问题不难解决.试题解析:(1)在
 中,
中,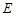 、
、 分别是
分别是 、
、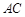 的中点,所以
的中点,所以 ,
,又
 平面
平面 ,
, 平面
平面 ,所以
,所以 平面
平面 . 6分
. 6分(2)在平面
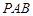 内过点
内过点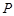 作
作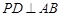 ,垂足为
,垂足为 .因为平面
.因为平面 平面
平面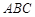 ,平面
,平面 平面
平面 ,
,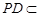 平面
平面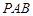 ,所以
,所以 平面
平面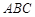 , 8分
, 8分又
 平面
平面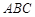 ,所以
,所以 , 10分
, 10分又
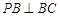 ,
, ,
,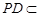 平面
平面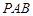 ,
, 平面
平面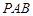 ,
,所以
 平面
平面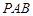 , 12分
, 12分又
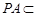 平面
平面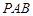 ,所以
,所以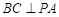 . 14分
. 14分

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 ACD沿AC折起至
ACD沿AC折起至 为600,G,H分别是PA,PC的中点.
为600,G,H分别是PA,PC的中点.

 平面BGH;
平面BGH;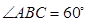 ,
,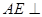 平面ABCD,
平面ABCD,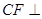 平面ABCD,
平面ABCD,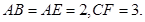
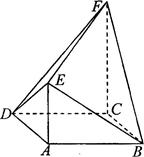
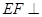 平面BDE;
平面BDE;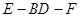 的大小.
的大小.

 是互不重合的直线,
是互不重合的直线, 是互不重合的平面,给出下列命题:
是互不重合的平面,给出下列命题: 则
则 或
或 ;
; 则
则 ;
; 不垂直于
不垂直于 ,则
,则 且
且 则
则
 ;
; 且
且 则
则 .
. 是三条不同的直线,
是三条不同的直线, 是三个不同的平面,下列命题:
是三个不同的平面,下列命题: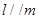 ,
,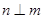 ,则
,则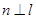 ; ②若
; ②若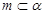 ,则
,则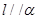 ;
;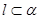 ,
,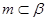 ,
,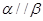 ,则
,则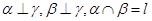 ,则
,则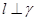 .
.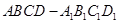 的棱长为
的棱长为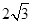 ,动点P在对角线
,动点P在对角线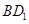 上,过点P作垂直于
上,过点P作垂直于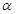 ,记这样得到的截面多边形(含三角形)的周长为y,设
,记这样得到的截面多边形(含三角形)的周长为y,设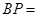 x,则当
x,则当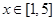 时,函数
时,函数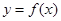 的值域为( )
的值域为( )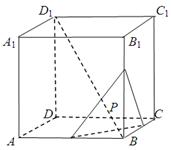
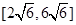
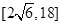
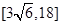
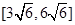
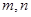 是两条不同的直线,
是两条不同的直线,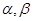 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( ) ,
,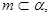
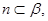 则
则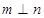
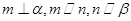 ,则
,则