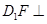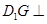题目内容
如图,正方体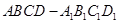 的棱长为
的棱长为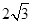 ,动点P在对角线
,动点P在对角线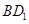 上,过点P作垂直于
上,过点P作垂直于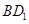 的平面
的平面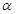 ,记这样得到的截面多边形(含三角形)的周长为y,设
,记这样得到的截面多边形(含三角形)的周长为y,设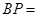 x,则当
x,则当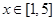 时,函数
时,函数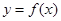 的值域为( )
的值域为( )
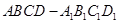 的棱长为
的棱长为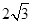 ,动点P在对角线
,动点P在对角线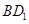 上,过点P作垂直于
上,过点P作垂直于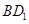 的平面
的平面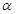 ,记这样得到的截面多边形(含三角形)的周长为y,设
,记这样得到的截面多边形(含三角形)的周长为y,设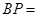 x,则当
x,则当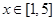 时,函数
时,函数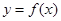 的值域为( )
的值域为( )
A.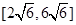 | B.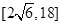 | C.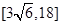 | D.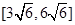 |
D
试题分析:棱长为
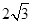 ,故体对角线
,故体对角线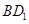 =
= ,根据对称性,只需研究
,根据对称性,只需研究 ,函数
,函数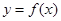 的值域,连接
的值域,连接 ,则
,则 面
面 ,此时
,此时 ,当
,当 时,截面周长为截面
时,截面周长为截面 周长的一半,即
周长的一半,即 ,当
,当 时,即当截面过体对角线
时,即当截面过体对角线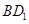 中点时,此时截面为正六边形,其顶点为个棱的中点,如图所示,截面周长为
中点时,此时截面为正六边形,其顶点为个棱的中点,如图所示,截面周长为 .,所以函数
.,所以函数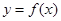 的值域为
的值域为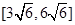 .
.

练习册系列答案
相关题目
 中,
中, 、
、 为棱
为棱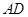 、
、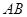 的中点.
的中点.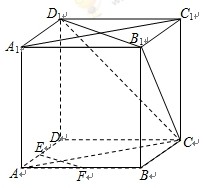
 ∥平面
∥平面 ;
; ⊥平面
⊥平面
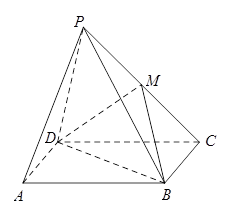
 中,点
中,点 分别是棱
分别是棱 的中点.
的中点.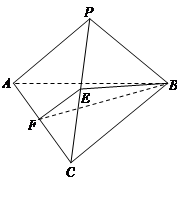
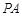 //平面
//平面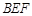 ;
; 平面
平面 ,
,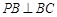 ,求证:
,求证: .
.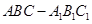 中,平面
中,平面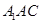 ⊥平面ABC,BC⊥AC,D为AC的中点,AC=BC=AA1=A1C=2。
⊥平面ABC,BC⊥AC,D为AC的中点,AC=BC=AA1=A1C=2。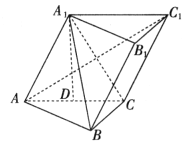
 中,底面
中,底面 是菱形,
是菱形,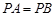 ,且侧面
,且侧面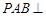 平面
平面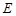 是棱
是棱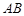 的中点.
的中点.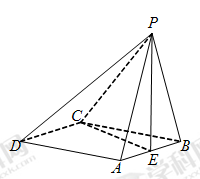
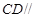 平面
平面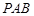 ;
;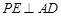 ;
;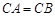 ,求证:平面
,求证:平面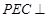 平面
平面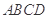 为正方形,
为正方形,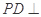 平面
平面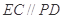 ,且
,且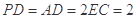
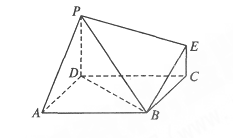
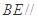 平面
平面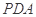 ;
; 的体积;
的体积;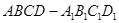 ,点
,点 ,
,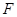 ,
,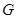 分别是线段
分别是线段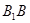 ,
,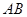 和
和 上的动点,观察直线
上的动点,观察直线 与
与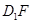 ,
,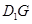 .给出下列结论:
.给出下列结论: