题目内容
在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥AB,△ABC是正三角形,AC与BD的交点M恰好是AC中点,N为线段PB的中点,G在线段BM上,且

(Ⅰ)求证:AB⊥PD;
(Ⅱ)求证:GN//平面PCD.


(Ⅰ)求证:AB⊥PD;
(Ⅱ)求证:GN//平面PCD.
(Ⅰ)证明:见解析;(Ⅱ)见解析.
试题分析:(Ⅰ)利用
 平面
平面 ,得到
,得到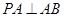 ,再由
,再由  ,即证得
,即证得 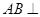 平面
平面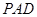 .由
.由 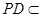 平面
平面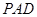 得证.
得证.(Ⅱ)根据
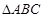 是正三角形,且
是正三角形,且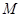 是
是 中点,
中点,可得
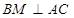 .
.在直角三角形
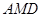 中,可得
中,可得 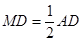 ,
,在直角三角形
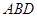 中,可得
中,可得 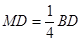 ,再根据
,再根据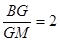 ,得到
,得到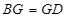 ,而
,而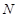 为线段
为线段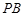 的中点, 得到
的中点, 得到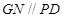 即可推出
即可推出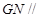 平面
平面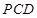 .
.试题解析:(Ⅰ)证明:因为
 平面
平面 ,所以
,所以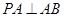 , 2分
, 2分又因为
 ,所以
,所以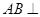 平面
平面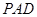 , 4分
, 4分又
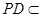 平面
平面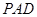 ,所以
,所以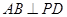 . 6分
. 6分
(Ⅱ)因为
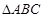 是正三角形,且
是正三角形,且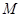 是
是 中点,
中点,所以
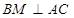 , 7分
, 7分在直角三角形
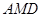 中,
中,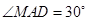 ,所以
,所以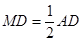 ,
,在直角三角形
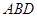 中,
中,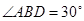 ,
,所以
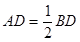 ,所以
,所以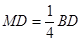 , 10分
, 10分又因为
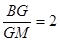 ,所以
,所以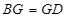 ,又
,又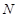 为线段
为线段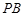 的中点,所以
的中点,所以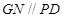 ,
,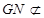 平面
平面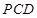 ,
,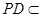 平面
平面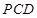 ,所以
,所以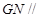 平面
平面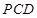 12分
12分
练习册系列答案
相关题目

 中,点
中,点 分别是棱
分别是棱 的中点.
的中点.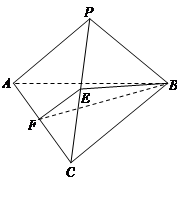
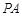 //平面
//平面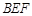 ;
; 平面
平面 ,
,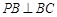 ,求证:
,求证: .
.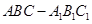 中,平面
中,平面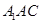 ⊥平面ABC,BC⊥AC,D为AC的中点,AC=BC=AA1=A1C=2。
⊥平面ABC,BC⊥AC,D为AC的中点,AC=BC=AA1=A1C=2。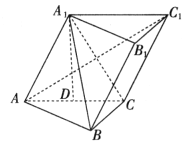
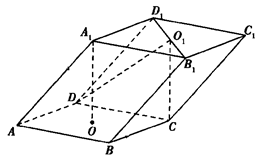
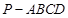 中,底面
中,底面 是菱形,
是菱形,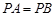 ,且侧面
,且侧面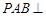 平面
平面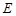 是棱
是棱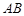 的中点.
的中点.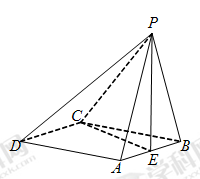
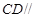 平面
平面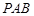 ;
;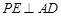 ;
;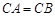 ,求证:平面
,求证:平面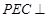 平面
平面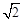 .
.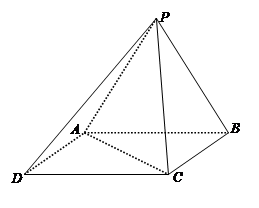
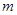 ,
,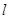 和平面
和平面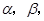 且
且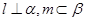 ,给出下列四个命题:
,给出下列四个命题: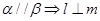 ②
②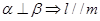 ③
③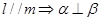 ④
④