题目内容
已知平行四边形ABCD(图1)中,AB=4,BC=5,对角线AC=3,将三角形 ACD沿AC折起至
ACD沿AC折起至 PAC位置(图2),使二面角
PAC位置(图2),使二面角 为600,G,H分别是PA,PC的中点.
为600,G,H分别是PA,PC的中点.


(1)求证:PC 平面BGH;
平面BGH;
(2)求平面PAB与平面BGH夹角的余弦值.
 ACD沿AC折起至
ACD沿AC折起至 PAC位置(图2),使二面角
PAC位置(图2),使二面角 为600,G,H分别是PA,PC的中点.
为600,G,H分别是PA,PC的中点.

(1)求证:PC
 平面BGH;
平面BGH;(2)求平面PAB与平面BGH夹角的余弦值.
(1)详见解析;(2)平面PAB与平面BGH夹角的余弦值 .
.
 .
.试题分析:(1)求证:
 平面
平面 ,证明线面垂直,只需证明线和平面内两条相交直线垂直即可,由于
,证明线面垂直,只需证明线和平面内两条相交直线垂直即可,由于 是
是 的中位线,,所以
的中位线,,所以 ,由已知
,由已知 ,对角线
,对角线 ,得
,得 ,从而可得
,从而可得 ,即
,即 ,即
,即 ,只需再找一条垂线即可,
,只需再找一条垂线即可,若
 问题得证,要证
问题得证,要证 ,只要
,只要 即可,由已知二面角
即可,由已知二面角 为600,可找二面角的平面角,故过C作
为600,可找二面角的平面角,故过C作 且
且 ,连
,连 ,则
,则 ,这样可证得
,这样可证得 ,从而得证;(2)求平面PAB与平面BGH夹角的余弦值,求二面角的大小,可采用向量法来求,以CE的中点O为原点,建立如图所示的空间直角坐标系,由题意可得各点的坐标,分别找出两个平面的法向量,即可求出平面PAB与平面BGH夹角的余弦值.
,从而得证;(2)求平面PAB与平面BGH夹角的余弦值,求二面角的大小,可采用向量法来求,以CE的中点O为原点,建立如图所示的空间直角坐标系,由题意可得各点的坐标,分别找出两个平面的法向量,即可求出平面PAB与平面BGH夹角的余弦值.试题解析:(1)证明:过C作
 且
且 ,连BE,PE
,连BE,PE
 ,
, 四边形
四边形 是矩形,
是矩形, ,
,
 平面PEC,
平面PEC,

 是正三角形
是正三角形
 平面PEC
平面PEC
 =5=BC,
=5=BC,而H是PC的中点,
 ,
, 是
是 的中位线,
的中位线, ,
,
 ,
, 平面BGH.
平面BGH.(2)以CE的中点O为原点,建立如图所示的空间直角坐标系,则
 ,
,
 ,
, ,
,先求平面PAB的法向量为
 ,而平面BGH的法向量为
,而平面BGH的法向量为 ,
,设平面PAB与平面BGH的夹角为
 ,则
,则 .
.

练习册系列答案
相关题目

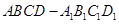 中,
中,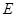 、
、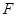 为棱
为棱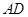 、
、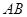 的中点.
的中点.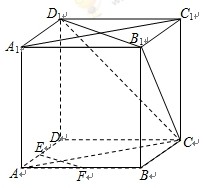
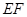 ∥平面
∥平面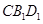 ;
;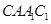 ⊥平面
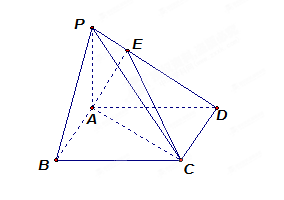
⊥平面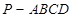 中,底面
中,底面 是边长为
是边长为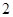 的正方形,
的正方形,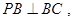
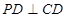 ,且
,且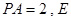 点满足
点满足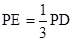 .
. 
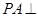 平面
平面 上是否存在点
上是否存在点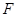 ,使得
,使得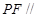 平面
平面 ?若存在,确定点
?若存在,确定点
 中,点
中,点 分别是棱
分别是棱 的中点.
的中点.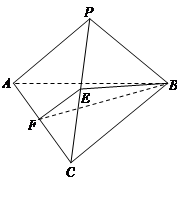
 //平面
//平面 ;
; 平面
平面 ,
,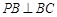 ,求证:
,求证: .
.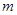 ,
,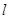 和平面
和平面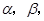 且
且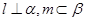 ,给出下列四个命题:
,给出下列四个命题: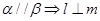 ②
②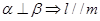 ③
③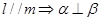 ④
④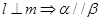
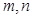 是不同的直线,
是不同的直线,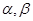 是不同的平面,下列命题中正确的是( )
是不同的平面,下列命题中正确的是( )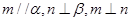 ,则
,则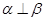
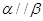
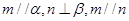 ,则
,则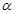 ⊥
⊥