Question

【题目】已知点E（﹣4，0）和F（4，0），过点E的直线l与过点F的直线m相交于点M，设直线l的斜率为k1，直线m的斜率为k2，如果k1k2．

（1）记点M形成的轨迹为曲线C，求曲线C的轨迹方程．

（2）已知P（2，m）、Q（2，﹣m）（m＞0）是曲线C上的两点，A，B是曲线C上位于直线PQ两侧的动点，当A，B运动时，满足∠APQ＝∠BPQ，试问直线AB的斜率是否为定值，请说明理由．

Answer 1

【答案】（1）（x≠）（2）直线AB的斜率为定值，详见解析

【解析】

(1)设点,再利用k1k2求得关于的方程即可.

(2)由∠APQ＝∠BPQ可知设直线PA的斜率为k,则PB的斜率为﹣k,再设直线PA的直线方程与椭圆联立,求得的坐标,再同理求得的坐标,再表达直线AB的斜率进行化简求解即可.

（1）设所求动点A（x,y）,由,,得,

又,∴,即（x≠±4）．

即点A的轨迹方程为（x≠±4）；

（2）当∠APQ＝∠BPQ,则PA、PB的斜率之和为0,设直线PA的斜率为k,

则PB的斜率为﹣k,

直线PA的直线方程为y﹣3＝k（x﹣2）,

由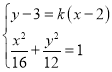,整理得（3+4k2）x2+8（3﹣2k）kx+4（3﹣2k）2﹣48＝0,

∴,

同理直线PB的直线方程为y﹣3＝﹣k（x﹣2）,

可得．

∴,,

∴,

∴直线AB的斜率为定值．