题目内容
12．若锐角α满足0°＜α＜45°，且sin2α=$\frac{\sqrt{3}}{2}$，tanα=$\frac{\sqrt{3}}{3}$．分析 利用已知条件求出角的大小，然后求解即可．
解答 解：锐角α满足0°＜α＜45°，且sin2α=$\frac{\sqrt{3}}{2}$，
可得α=$\frac{π}{6}$，
tanα=tan$\frac{π}{6}$=$\frac{\sqrt{3}}{3}$．
故答案为：$\frac{\sqrt{3}}{3}$．
点评 本题考查三角函数的化简求值，可以利用二倍角公式以及同角三角函数的基本关系式求解，但是比较麻烦．
练习册系列答案
相关题目
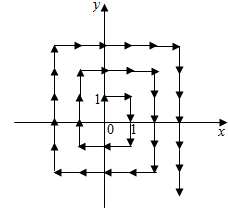如图，将自然数按如下规则“放置”在平面直角坐标系中，使其满足条件：①每个自然数“放置”在一个“整点”（横纵坐标均为整数的点）上；②0在原点，1在（0，1）点，2在（1，1）点，3在（1，0）点，4在（1，-1）点，5在（0，-1）点，…，即所有自然数按顺时针“缠绕”在以“0”为中心的“桩”上，则放置数字（2n+1）2，n∈N*的整点坐标是（-n，n+1）．
20．已知全集U={x|x≤3}，A={x|x+1＜0}，B={x|y=lnx}，则（∁UA）∪B=（ ）
| A． | [-1，3] | B． | （0，3] | C． | （0，+∞） | D． | [-1，+∞） |