题目内容
6.已知函数f(x)为定义在R上的奇函数,当x>0时,f(x)=-x2+4x,(1)求f(x)的解析式
(2)若函数f(x)在区间[-1,a-2]上单调递增,求实数a的取值范围.
分析 (1)先求f(0)=0,再设x<0,由奇函数的性质f(x)=-f(-x),利用x>0时的表达式求出x<0时函数的表达式.
(2)函数f(x)在区间[-1,a-2]上单调递增,可得-1<a-2≤2,即可求实数a的取值范围.
解答 解:(1)∵函数f(x)是定义在R上的奇函数,
∴f(0)=0,且f(-x)=-f(x),
∴f(x)=-f(-x),
设x<0,则-x>0,
∴f(-x)=-x2-4x,
∴f(x)=-f(-x)=-(-x2-4x)=x2+4x,
∴f(x)=$\left\{\begin{array}{l}{{x}^{2}+4x,x≤0}\\{-{x}^{2}+4x,x>0}\end{array}\right.$;
(2)∵函数f(x)在区间[-1,a-2]上单调递增,
∴-1<a-2≤2,
∴1<a≤4.
点评 本题主要考查奇函数的性质求解函数的解析式,关键是利用原点两侧的函数表达式之间的关系解题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
3.某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序对三名候选人进行了笔试和面试,成绩最高的将被推荐.各项成绩如下表所示:请你根据表中信息解答下列问题:
(1)若按笔试和面试的平均得分确定最后成绩,应当推荐谁?
(2)若笔试、面试两项得分按照6:4的比确定最后成绩,应当推荐谁?
| 测试项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 92 | 85 | 95 |
| 面试 | 85 | 95 | 80 |
(2)若笔试、面试两项得分按照6:4的比确定最后成绩,应当推荐谁?
4.若(2-x)2013=a0+a1x+a2x2+…+a2013x2013,则$\frac{{a}_{0}+{a}_{2}+{a}_{4}+…{+a}_{2012}}{{a}_{1}+{a}_{3}+{a}_{5}+…+{a}_{2013}}$=( )
| A. | $\frac{{3}^{2013}+1}{{3}^{2013}-1}$ | B. | -$\frac{{3}^{2013}+1}{{3}^{2013}-1}$ | ||
| C. | $\frac{{3}^{2012}+1}{{3}^{2012}-1}$ | D. | -$\frac{{3}^{2012}+1}{{3}^{2012}-1}$ |
1.若θ为第二象限角,那么sin(cos2θ)•cos(sin2θ)的值为( )
| A. | 正值 | B. | 负值 | C. | 零 | D. | 以上都有可能 |
18.等比数列{an}的前4项和为4,前12项和为28,则它的前8项和是( )
| A. | -8 | B. | 12 | C. | -8或12 | D. | 8 |
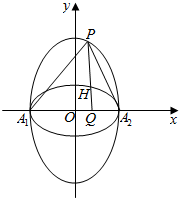 若两个椭圆的离心率相等,则称它们为“相似椭圆”.如图,在直角坐标系xOy中,已知椭圆C1:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1,A1,A2分别为椭圆C1的左右顶点,椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”
若两个椭圆的离心率相等,则称它们为“相似椭圆”.如图,在直角坐标系xOy中,已知椭圆C1:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1,A1,A2分别为椭圆C1的左右顶点,椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”