题目内容
6.设方程3-x=|lgx|的两个根分别为x1,x2,则( )| A. | x1x2<0 | B. | x1x2=1 | C. | x1x2>1 | D. | 0<x1x2<1 |
分析 构造f(x)=($\frac{1}{3}$)x,g(x)=|lgx|,画出图象,求解f($\frac{1}{2}$)=$\frac{1}{\sqrt{3}}$,g($\frac{1}{2}$)=lg2=0.3010
f(2)=$\frac{1}{9}$,g(2)=lg2=0.3010,利用根的存在性定理得出即可.
解答 解;f(x)=($\frac{1}{3}$)x,g(x)=|lgx|的图象为
∵f($\frac{1}{2}$)=$\frac{1}{\sqrt{3}}$,g($\frac{1}{2}$)=lg2=0.3010
f(2)=$\frac{1}{9}$,g(2)=lg2=0.3010
f($\frac{1}{2}$)>g($\frac{1}{2}$),f(2)<g(2)根据根的存在性定理得出
0<x1$<\frac{1}{2}$,1<x2<2,
∴0<x1x2<1
故选:D
点评 本题考察了函数的图象的运用,判断方程的根的问题,属于中档题,利用好根的存在性定理.

练习册系列答案
相关题目
1.若函数y=log${\;}_{\frac{1}{2}}$(3x2-6x十5)在[a,+∞)上是减函数,则实数a的取值范围是( )
| A. | [1,+∞) | B. | [2,+∞) | C. | (-∞,2] | D. | (-∞,1] |
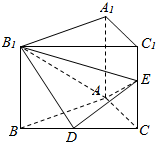 如图,在直三棱柱ABC-A1B1C1中,D,E分别是BC和CC1的中点,已知AB=AC=AA1=4,∠BAC=90°.
如图,在直三棱柱ABC-A1B1C1中,D,E分别是BC和CC1的中点,已知AB=AC=AA1=4,∠BAC=90°.



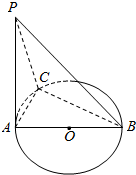 AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点.
AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点.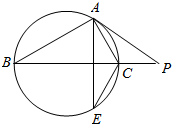 若图中,PA切⊙O于点A,PCB交⊙O于C、B两点,且PCB过点O,AE⊥BP交⊙O于E,则图中与∠CAP相等的角的个数是( )
若图中,PA切⊙O于点A,PCB交⊙O于C、B两点,且PCB过点O,AE⊥BP交⊙O于E,则图中与∠CAP相等的角的个数是( )