Question

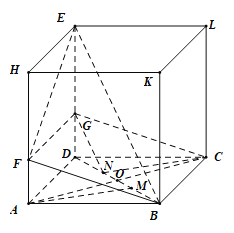
【题目】如图，在长方体ABCD﹣HKLE中，底面ABCD是边长为3的正方形，对角线AC与BD相交于点O，点F在线段AH上且，BE与底面ABCD所成角为.

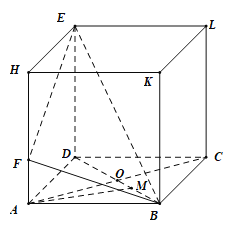
（1）求证：AC⊥BE；

（2）M为线段BD上一点，且，求异面直线AM与BF所成角的余弦值.

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）推导出DE⊥AC，AC⊥BD，从而AC⊥平面BDE.由此能证明AC⊥BE.

（2）推导出∠DBE为直线BE与平面ABCD所成的角，∠DBE，在DE上取一点G，使DGDE，连接FG，则四边形FBCG为平行四边形，BF∥CG，在BD上取一点N，使DN＝BM，推导出AM∥CN，从而∠GCN（或其补角）为异面直线AM与BF所成的角，由余弦定理能求出异面直线AM与BF所成角的余弦值.

解：（1）证明：因为在长方体ABCD﹣HKLE中，有DE⊥平面ABCD，

所以DE⊥AC，

因为四边形ABCD是正方形，所以AC⊥BD，

又BD∩DE＝D，从而AC⊥平面BDE.

而BE平面BDE，

所以AC⊥BE.

（2）因为在长方体ABCD﹣HKLE中，有BE与平面ABCD所成角为，

由（1）知∠DBE为直线BE与平面ABCD所成的角，

所以∠DBE，

所以.

由AD＝3可知，

所以AH＝3，

又2，

即AFAH，

故，

在DE上取一点G，使DGDE，

连接FG，

则在长方体ABCD﹣HKLE中，有FG∥AD∥BC，

且FG＝AD＝BC，

所以四边形FBCG为平行四边形，

所以BF∥CG，

在BD上取一点N，使DN＝BM，

因为BM，BD＝3，

所以DN＝BM，

所以在正方形ABCD中，ON＝OM，

所以△CON≌△AOM，

所以∠CNO＝∠，

所以AM∥CN，

所以∠GCN（或其补角）为异面直线AM与BF所成的角，

在△GNC中，GC＝BF，

在△AMB中，由余弦定理得AM，

则CN＝AM，

又GN2，

在△GNC中，由余弦定理得：

cos∠GCN.

故异面直线AM与BF所成角的余弦值为.