题目内容

对任意实数a∈[
2
，+∞），点P（a，2-a）与圆C：x2+y2-4y=0的位置关系是（　　）
A、点P在圆上
B、点P在圆外
C、点P在圆内 或圆上
D、点P在圆外或圆上
考点：点与圆的位置关系
专题：直线与圆
分析：求出|CP|的长与圆半径相比较，能确定点P（a，2-a）与圆C：x2+y2-4y=0的位置关系．
解答： 解：∵a∈[
2
，+∞），P（a，2-a），
圆C：x2+y2-4y=0的圆心C（0，2），半径r=
1
2
16
=2，
|PC|=
a2+a2
=
2
a≥2
2
＞r=2，
∴点P（a，2-a）在圆外．
故选：B．
点评：本题考查点与圆的位置关系的判断，是基础题，解题时要认真审题，注意圆的性质的合理运用．
练习册系列答案
相关题目
设函数f（x）=sinxcos（x+
π
3
）+
3
4
，x∈R．
（Ⅰ）求f（x）的最大值及最小正周期；
（Ⅱ）讨论f（x）在区间[0，
π
2
]上的单调性．
已知函数f（x）=ax+
1
a
（1-x）（a＞0），且f（x）在[0，1]上的最小值为g（a），求g（a）的最大值．
定义在R上的函数f（x）满足：f′（x）＞1-f（x），f（0）=6，f′（x）是f（x）的导函数，则不等式exf（x）＞ex+5（其中e为自然对数的底数）的解集为
 
．
已知定义在R上的单调函数f（x）满足：存在实数x0，使得对于任意实数x1，x2，总有f（x0x1+x0x2）=f（x0）+f（x1）+f（x2）恒成立．求：
（1）f（1）+f（0）；  
（2）x0的值．
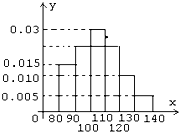某校高一某班共有64名学生，如图是该班某次数学考试成绩的频率分布直方图，根据该图可知，成绩在110-120间的同学大约有（　　）
A、10B、11C、13D、16
若点（2，k）到直线5x-12y+6=0的距离是4，则k的值是（　　）
A、1
B、-3
C、1或
5
2
D、-3或
17
3
[81-0.25+(
33
8
)-
1
3
]
1
2
+
1
2
lg4-lg
1
5
=
 
．
设S、T是R的两个非空子集，如果存在一个从S到T的函数y=f（x）满足：
（i）T={f（x）|x∈S}；
（ii）对任意x1，x2∈S，当x1＜x2时，恒有f（x1）＜f（x2）．
那么称这两个集合“保序同构”．现给出以下4对集合：
①S=R，T={-1，1}；  
②S={x|-1≤x≤1}，T=R；
③S=N，T=N*；       
④S=R，T={x|x＜0}
其中，“保序同构”的集合对的序号是
 
（写出“保序同构”的集合对的序号）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网