题目内容
若1,a,b,c,9成等比数列,则( )
| A、b=3,ac=9 |
| B、b=-3,ac=9 |
| C、b=3,ac=-9 |
| D、b=-3,ac=-9 |
考点:等比数列的性质
专题:等差数列与等比数列
分析:根据等比数列的首项和末项求出q2=3,再由通项公式求出第三项b,由性质求出ac的值.
解答:
解:设等比数列1,a,b,c,9的公比是q,
则q4=
=9,即q2=3,
所以第三项b=1×q2=3,ac=1×9=9,
故选:A.
则q4=
| 9 |
| 1 |
所以第三项b=1×q2=3,ac=1×9=9,
故选:A.
点评:本题考查等比数列的通项公式,以及性质的应用,注意公比的符号,考查的整体代换思想.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
高三年级的三个班去甲、乙、丙、丁四个工厂参加社会实践,但去何工厂可自由选择,甲工厂必须有班级要去,则不同的分配方案有( )
| A、16种 | B、18种 |
| C、37种 | D、48种 |
在区间[0,10]中任意取一个数,则它与4之和大于10的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)的定义域为R,其导函数f′(x)的图象如图所示,则函数f(x)( )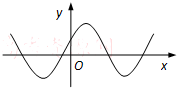

| A、有三个极值点,但无法判断有几个极大值,几个极小值 |
| B、有一个极大值点,两个极小值点 |
| C、有两个极大值点,两个极小值点 |
| D、有四个极值点,但无法判断有几个极大值,几个极小值 |
若函数f(x)=lnx-1,则f′(1)=( )
| A、0 | B、1 | C、-1 | D、e |
在相距4千米的A、B两点处测量目标C,若∠CAB=75°,∠CBA=60°,则A、C两点之间的距离是( )
| A、4千米 | ||
B、2
| ||
C、2
| ||
| D、2千米 |
已知点(-1,-1)在直线ax+by+2=0(a>0,b>0)上,则
+
的最小值为( )
| 1 |
| a |
| 1 |
| b |
| A、1 | B、2 | C、3 | D、4 |