题目内容
已知数列{an}满足an+1=an-an-1(n≥2),a1=1,a2=3,记Sn=a1+a2+…+an,则下列结论正确的是( )
A.a2 014=-1,S2 014=2 B.a2 014=-3,S2 014=5
C.a2 014=-3,S2 014=2 D.a2 014=-1,S2 014=5
D
[解析] 由已知数列{an}满足an+1=an-an-1(n≥2),知an+2=an+1-an,an+2=-an-1(n≥2),an+3=-an,an+6=an,又a1=1,a2=3,a3=2,a4=-1,a5=-3,a6=-2,
所以当k∈N时,ak+1+ak+2+ak+3+ak+4+ak+5+ak+6=a1+a2+a3+a4+a5+a6=0,a2 014=a4=-1,S2 014=a1+a2+a3+a4=1+3+2+(-1)=5,故选D.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 要使函数
要使函数 上存在反函数,则a的取值范围是___________
上存在反函数,则a的取值范围是___________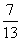 (0<α<π),则tan α=( )
(0<α<π),则tan α=( )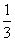 B.
B.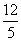 C.-
C.-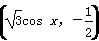 ,函数f(x)=(a+b)·a-2.
,函数f(x)=(a+b)·a-2. ,c=4,且f(A)=1,求△ABC的面积S.
,c=4,且f(A)=1,求△ABC的面积S.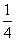 C.
C.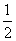 D.1
D.1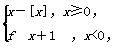 其中[x]表示不超过x的最大整数,如[-1.1]=-2,[π]=3.若直线y=kx+k(k>0)与函数f(x)的图象恰好有3个不同的交点,则实数k的取值范围是( )
其中[x]表示不超过x的最大整数,如[-1.1]=-2,[π]=3.若直线y=kx+k(k>0)与函数f(x)的图象恰好有3个不同的交点,则实数k的取值范围是( )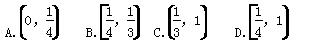
 ,若f(2)=3,则实数a的值为
,若f(2)=3,则实数a的值为