题目内容
20.复数z满足zi=1-$\sqrt{5}$i(i为虚数单位),则z等于( )| A. | -$\sqrt{5}$-i | B. | $\sqrt{5}$-i | C. | i | D. | -i |
分析 把已知等式变形,利用复数代数形式的乘除运算化简得答案.
解答 解:∵zi=1-$\sqrt{5}$i,
∴$z=\frac{1-\sqrt{5}i}{i}=\frac{(1-\sqrt{5}i)(-i)}{-{i}^{2}}=-\sqrt{5}-i$.
故选:A.
点评 本题考查复数代数形式的乘除运算,是基础的计算题.

练习册系列答案
相关题目
10.直线l过抛物线C:y2=2px(p>0)的焦点且与x轴垂直,l与C交于A、B两点,P为C的准线上一点,若△ABP的面积为36,则p的值为( )
| A. | 3 | B. | 6 | C. | 12 | D. | 6$\sqrt{2}$ |
8.若函数f(x)=$\frac{{a{x^2}}}{2}-({1+2a})x+2lnx({a>0})$在区间$({\frac{1}{2},1})$内有极大值,则a的取值范围是( )
| A. | $({\frac{1}{e},+∞})$ | B. | (1,+∞) | C. | (1,2) | D. | (2,+∞) |
12.集合A={x|-2≤x≤3},B={x|x<-1},则A∩(∁RB)等于( )
| A. | {x|x>-1} | B. | {x|x≥-1} | C. | {x|-2≤x≤-1} | D. | {x|-1≤x≤3} |
9.已知等边三角形的一个顶点位于原点,另外两个顶点在抛物线y2=2$\sqrt{3}$x上,则这个等边三角形的边长为( )
| A. | 6$\sqrt{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | 6 | D. | 12 |
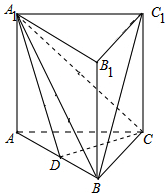 如图,在三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形,D为AB中点.
如图,在三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形,D为AB中点.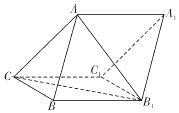 如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AC=AB1.
如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AC=AB1.