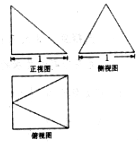
题目内容
15.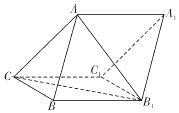 如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AC=AB1.
如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AC=AB1.(1)证明:AB⊥B1C;
(2)若$B{B_1}=a,∠CB{B_1}=\frac{2π}{3}$,平面AB1C⊥平面BB1C1C,直线AB与平面BB1C1C所成角为$\frac{π}{4}$,求点B1到平面ABC的距离.
分析 (1)连结BC1交B1C于O,连结AO,说明B1C⊥BC1,AO⊥B1C,证明B1C⊥平面ABO,即可推出AB⊥B1C.
(2)证明AO⊥平面BB1C1C.得到$∠ABO=\frac{π}{4}$,求出${V_{A-{B_1}BC}}=\frac{1}{3}×\frac{1}{2}×\sqrt{3}a×\frac{1}{2}a×\frac{1}{2}a=\frac{{\sqrt{3}}}{24}{a^3}$,设B1到平面ABC的距离为h,利用等体积法,转化求解即可.
解答  解:(1)证明:连结BC1交B1C于O,连结AO,
解:(1)证明:连结BC1交B1C于O,连结AO,
在菱形BB1C1C中,B1C⊥BC1,
∵AC=AB1,O为B1C中点,
∴AO⊥B1C,
又∵AO∩BC1=0,
∴B1C⊥平面ABO,
∴AB⊥B1C.
(2)∵平面AB1C⊥平面BB1C1C,平面AB1C∩平面BB1C1C=B1C,又AO⊥B1C,
∴AO⊥平面BB1C1C.
∴$∠ABO=\frac{π}{4}$,
∵BB1=a,$∠CB{B_1}=\frac{2π}{3}$,
∴$B{C_1}=a,BO=\frac{a}{2}$,故$AO=\frac{a}{2},AB=\frac{{\sqrt{2}}}{2}a,CO=\frac{{\sqrt{3}}}{2}a,AC=a$.
∴${V_{A-{B_1}BC}}=\frac{1}{3}×\frac{1}{2}×\sqrt{3}a×\frac{1}{2}a×\frac{1}{2}a=\frac{{\sqrt{3}}}{24}{a^3}$,
∵△ABC为等腰三角形,∴${S_{△ABC}}=\frac{{\sqrt{7}}}{8}{a^2}$.
设B1到平面ABC的距离为h,则${V_{A-{B_1}BC}}={V_{{B_1}-ABC}}=\frac{1}{3}×\frac{{\sqrt{7}}}{8}{a^2}×h=\frac{{\sqrt{7}}}{24}{a^2}•h=\frac{{\sqrt{3}}}{24}{a^3}$,
∴$h=\frac{{\sqrt{21}}}{7}a$.
点评 本题考查直线与平面垂直的判定定理以及性质定理的应用,几何体的体积的求法,考查计算能力以及空间想象能力.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案| A. | (2,3) | B. | (-2,3) | C. | (-2,-3) | D. | (2,-3) |
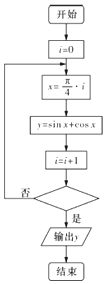
| A. | i>5? | B. | i>3? | C. | i>6? | D. | i>4? |
| A. | -$\sqrt{5}$-i | B. | $\sqrt{5}$-i | C. | i | D. | -i |
 如图,在棱柱ABC-A1B1C1中,点C在平面A1B1C1内的射影点为的A1B1中点O,AC=BC=AA1,∠ACB=90°.
如图,在棱柱ABC-A1B1C1中,点C在平面A1B1C1内的射影点为的A1B1中点O,AC=BC=AA1,∠ACB=90°.(1)求证:AB⊥平面OCC1;
(2)求二面角A-CC1-B的正弦值.
| A. | 0 | B. | $\frac{π}{4}$ | C. | -$\frac{π}{4}$ | D. | $\frac{3π}{4}$ |