题目内容
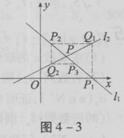
如图,直线l1:y=kx+1-k(k≠0,k≠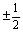 )与l2相交于点P.直线l1与x轴交于点P1,过点P1作x轴的垂线交于直线l2于点Q1,过点Q1作y轴的垂线交直线l1于点P2,过点P2作x轴的垂线交直线l2于点Q2,…这样一直作下去,可得到一系列点P1,Q1,P2,Q2,…点Pn(n=1,2,…)的横坐标构成数列{xn}.
)与l2相交于点P.直线l1与x轴交于点P1,过点P1作x轴的垂线交于直线l2于点Q1,过点Q1作y轴的垂线交直线l1于点P2,过点P2作x轴的垂线交直线l2于点Q2,…这样一直作下去,可得到一系列点P1,Q1,P2,Q2,…点Pn(n=1,2,…)的横坐标构成数列{xn}.
(Ⅰ)证明xn+1-1=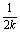 (xn-1),(n∈N*);
(xn-1),(n∈N*);
(Ⅱ)求数列{xn}的通项公式;
(Ⅲ)比较2|PPn|2与4k2|PP1|2+5的大小.
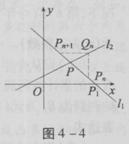 (Ⅱ)解法:由题设知x1=1-
(Ⅱ)解法:由题设知x1=1-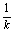 ,x1-1=-
,x1-1=-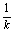 ≠0,又由(Ⅰ)知xn+1-1=
≠0,又由(Ⅰ)知xn+1-1=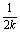 (xn-1), 所以数列{xn-1}是首项为x1-1,公比为
(xn-1), 所以数列{xn-1}是首项为x1-1,公比为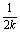 的等比数列.从而xn-1=-
的等比数列.从而xn-1=-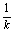 ×(
×(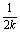 )n-1,即xn=1-2×(
)n-1,即xn=1-2×(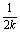 )n,n∈N*.
)n,n∈N*.
(Ⅲ)解法:由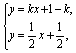 得点P的坐标为(1,1).所以
得点P的坐标为(1,1).所以
2|PPn|2=2(xn-1)2+2(kxn+1-k-1)2=8×(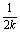 )2n+2(2
)2n+2(2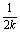 )2
)2 n-2,4k2|PP1|2+5=
n-2,4k2|PP1|2+5=
4k2[(1-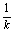 -1)2(0-1)2]+5=4k2+9.
-1)2(0-1)2]+5=4k2+9.
(i)当|k|> ,即k<-
,即k<- 或k>
或k> 时,4k2 |PP1|2+5>1+9=10.D而此时0<|
时,4k2 |PP1|2+5>1+9=10.D而此时0<|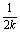 |<1,所以2|PPn|2<8×1+2=10,故2|PPn|2<4k2|PP1|2+5.
|<1,所以2|PPn|2<8×1+2=10,故2|PPn|2<4k2|PP1|2+5.
(ii)当0<|k|< ,即k∈(-
,即k∈(- ,0)∪(0,
,0)∪(0, )时,4k2|PP1|2+5<1+9=10.而此时|
)时,4k2|PP1|2+5<1+9=10.而此时|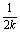 |>1,所以2|PPN|2>8×1+2=10.故2|PPn|2>4k2|PP1|2+5.
|>1,所以2|PPN|2>8×1+2=10.故2|PPn|2>4k2|PP1|2+5.

练习册系列答案
相关题目
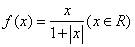 时,分别给出下面几个结论:
时,分别给出下面几个结论: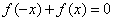 对
对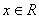 恒成立;(2)函数
恒成立;(2)函数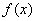 的值域为(-1,1);
的值域为(-1,1);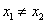 ,则一定有
,则一定有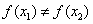 ;(4)函数
;(4)函数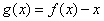 在R上有三个零点
在R上有三个零点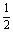 .试问,此人距山崖的水平距离多远时,观看塔的视角∠BPC最大(不计此人的身高)?
.试问,此人距山崖的水平距离多远时,观看塔的视角∠BPC最大(不计此人的身高)?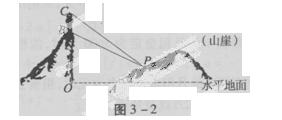
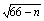 .其中m为每吨煤的价格,n为每百度电的价格;如果烧煤时的费用不超过用电炉时的费用,则用煤烧水;否则就用电炉烧水.
.其中m为每吨煤的价格,n为每百度电的价格;如果烧煤时的费用不超过用电炉时的费用,则用煤烧水;否则就用电炉烧水.
 或4
或4 

 上的可导函数
上的可导函数 ,恒有
,恒有 ,(其中
,(其中 表示函数
表示函数 在
在 的值),则
的值),则 分别是椭圆
分别是椭圆 的左右焦点,过
的左右焦点,过 的直线L与E相交于A,B两点且
的直线L与E相交于A,B两点且 成等差数列,则
成等差数列,则
 。
。