题目内容
已知数列{an}的前n项和Sn=a[2-( )n-1]-b[2-(n+1)(
)n-1]-b[2-(n+1)( )n-1](n=1,2,…),其中a,b是非零常数,则存在数列{xn}、{yn}使得( )
)n-1](n=1,2,…),其中a,b是非零常数,则存在数列{xn}、{yn}使得( )
A.an=xn+yn,其中{xn}为等差数列,{yn}为等比数列
B.an=xn+yn,其中{xn}和{yn}都为等差数列
C.an=xn·yn,其中{xn}为等差数列,{yn}为等比数列
D.an=xn·yn,其中{xn}和{yn}都为等比数列
C.
a1=S1=3a an=Sn-Sn-1=a[2+( )n-1]-b[2-(n+1)·(
)n-1]-b[2-(n+1)·( )n+1]-a[2+(
)n+1]-a[2+( )n-2]+b[2-n(
)n-2]+b[2-n( )n-2]=(bn-b-a)·(
)n-2]=(bn-b-a)·( )n-1 ∵{(
)n-1 ∵{( )n-1}为等比数列,{bn-a-b}为等差数列.
)n-1}为等比数列,{bn-a-b}为等差数列.

练习册系列答案
相关题目
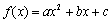 (a≠0),且方程
(a≠0),且方程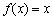 无实根。现有四个命题①若
无实根。现有四个命题①若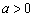 ,则不等式
,则不等式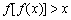 对一切
对一切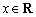 成立;②若
成立;②若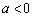 ,则必存在实数
,则必存在实数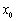 使不等式
使不等式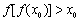 成立;③方程
成立;③方程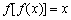 一定没有实数根;④若
一定没有实数根;④若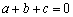 ,则不等式
,则不等式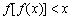 对一切
对一切 3x2-logax<0的解集为{x|0<x<
3x2-logax<0的解集为{x|0<x<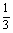 =的非空子集,则实数a的取值范围是 ( )
=的非空子集,则实数a的取值范围是 ( )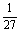 ,1] B.(
,1] B.(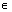 N.
N.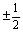 )与l2相交于点P.直线l1与x轴交于点P1,过点P1作x轴的垂线交于直线l2于点Q1,过点Q1作y轴的垂线交直线l1于点P2,过点P2作x轴的垂线交直线l2于点Q2,…这样一直作下去,可得到一系列点P1,Q1,P2,Q2,…点Pn(n=1,2,…)的横坐标构成数列{xn}.
)与l2相交于点P.直线l1与x轴交于点P1,过点P1作x轴的垂线交于直线l2于点Q1,过点Q1作y轴的垂线交直线l1于点P2,过点P2作x轴的垂线交直线l2于点Q2,…这样一直作下去,可得到一系列点P1,Q1,P2,Q2,…点Pn(n=1,2,…)的横坐标构成数列{xn}.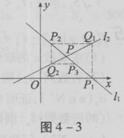
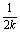 (xn-1),(n∈N*);
(xn-1),(n∈N*);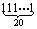 )2转换成十进制数是 .
)2转换成十进制数是 .  的焦点为
的焦点为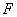 ,顶点为
,顶点为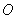 ,准线为
,准线为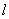 ,过该抛物线上异于顶点
,过该抛物线上异于顶点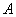 作
作 于点
于点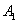 ,以线段
,以线段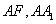 为邻边作平行四边形
为邻边作平行四边形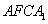 ,连接直线
,连接直线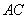 交
交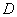 ,延长
,延长 交抛物线于另一点
交抛物线于另一点 。若
。若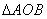 的面积为
的面积为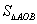 ,
,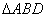 的面积为
的面积为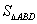 ,则
,则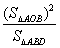 的最大值为____________。
的最大值为____________。