题目内容
20．已知P（1，1）为椭圆2x2+y2=4内一定点，过P引一条弦，使此弦以P为中点，则弦所在的直线方程2x+y-3=0．分析 方法一：设A和B点坐标，代入椭圆方程，作差，根据直线的斜率公式，即可求得直线的斜率，利用点差法即可求得直线AB的方程；
方法二：设A（1+m，1+n），B（1-m，1-n），代入椭圆方程，作差，求得2m+n=0，AB的斜率k=$\frac{n}{m}$=-2，利用点差法即可求得直线AB的方程；
解答 解：方法一：设此弦的端点为A（x1，y1），B（x2，y2）．
则2x12+y12=4，2x22+y22=4，相减可得：2（x1+x2）（x1-x2）+（y1+y2）（y1-y2）=0．
∵x1+x2=2，y1+y2=2，
∴2（x1-x2）+（y1-y2）=0，
∴k=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-2，
∴此弦所在的直线方程为y-1=-2（x-1），即2x+y-3=0．
故答案为：2x+y-3=0．
方法二：设以P（1，1）为中点的弦与椭圆交于A（1+m，1+n），B（1-m，1-n），
∴2（1+m）2+（1+n）2=4，2（1-m）2+（1-n）2=4，
两式相减得：2×2×2m+2×2n=0，则2m+n=0，
则AB的斜率k=$\frac{n}{m}$=-2，
此弦所在的直线方程为y-1=-2（x-1），即2x+y-3=0．
故答案为：2x+y-3=0．
点评 本题考查了椭圆的标准方程及其性质、中点坐标公式与斜率计算公式、“点差法”，考查了推理能力与计算能力，属于中档题．
练习册系列答案
优百分课时互动系列答案
相关题目
11．要从8名男医生和7名女医生中选5人组成一个医疗队，如果其中至少有2名男医生和至少有2名女医生，则不同的选法种数为（ ）
| A． | （C${\;}_{8}^{3}$+C${\;}_{7}^{2}$）（C${\;}_{7}^{3}$+C${\;}_{8}^{2}$） | B． | （C${\;}_{8}^{3}$+C${\;}_{7}^{2}$）+（C${\;}_{7}^{3}$+C${\;}_{8}^{2}$） | ||
| C． | C${\;}_{8}^{3}$C${\;}_{7}^{2}$+C${\;}_{7}^{3}$C${\;}_{8}^{2}$ | D． | C${\;}_{8}^{3}$C${\;}_{7}^{2}$+C${\;}_{7}^{3}$+C${\;}_{11}^{1}$ |
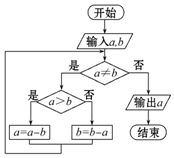某同学根据“更相减损术”设计出程序框图（图）．若输入a的值为98，b的值为63，则执行该程序框图输出的结果为（ ）
如图，四棱锥P-ABCD，底面ABCD是边长为2的菱形，$∠ABC=\frac{π}{3}$，且PA⊥平面ABCD．
在某小学体育素质达标运动会上，对10名男生和10名女生在一分钟跳绳的次数进行统计，得到如下所示茎叶图：