题目内容

10．函数y=$\frac{{2}^{x}+a}{{2}^{x}+1}$是增函数．则a的取值范围是a＜1．

分析 根据指数函数的单调性，和函数单调性的性质，结合已知中函数y=$\frac{{2}^{x}+a}{{2}^{x}+1}$为增函数，可得y=$\frac{a-1}{{2}^{x}+1}$为增函数，进而a-1＜0．

解答 解：函数y=$\frac{{2}^{x}+a}{{2}^{x}+1}$=1+$\frac{a-1}{{2}^{x}+1}$为增函数，
则y=$\frac{a-1}{{2}^{x}+1}$为增函数，
故a-1＜0，
解得：a＜1．
故答案为：a＜1

点评 本题考查的知识点是函数单调性的性质，指数函数的单调性，难度中档．

练习册系列答案
相关题目
20．已知n∈N*，在（x+2）n的展开式中，第二项系数是第三项系数的$\frac{1}{5}$．
（1）求n的值；
（2）求展开式中二项式系数最大的项；
（3）若（x+2）n=a0+a1（x+1）+a2（x+1）2+…+an（x+1）n，求a0+a1+…+an的值．
1．设A={直角三角形}，B={等腰三角形}，C={等边三角形}，D={等腰直角三角形}，则下列结论不正确的是（　　）
A．A∩B=DB．A∩D=DC．B∩C=CD．A∪B=D
18．“角α≠$\frac{π}{4}$”是“tanα≠1”的（　　）
A．充分不必要条件B．必要不充分条件C．充要条件D．以上都不对
5．已知函数f（x）=$\left\{\begin{array}{l}{2x-1（x＞-1）}\\{{e}^{x}（x≤-1）}\end{array}\right.$，若a＜b，f（a）=f（b），则实数a-2b的取值范围为（　　）
A．（-∞，$\frac{1}{e}$-1）B．（-∞，1-$\frac{1}{e}$）C．（-∞，2-$\frac{1}{e}$）D．（-∞，-$\frac{1}{e}$-2）
15．已知f（x）=$\frac{x}{1+x}$，则f（1）+f（2）+f（3）+f（4）+…+f（2016）+f（$\frac{1}{2}$）+f（$\frac{1}{3}$）+f（$\frac{1}{4}$）+…f（$\frac{1}{2016}$）=$\frac{4031}{2}$．
2．$\frac{1}{{log}_{2}3}$-$\frac{1}{{log}_{4}3}$+$\frac{1}{{log}_{6}3}$的值是1．
19．若函数f（x）定义域内有两个任意实数x1，x2（x1≠x2），若$f（\frac{{{x_1}+{x_2}}}{2}）$＜$\frac{{f（{x_1}）+f（{x_2}）}}{2}$恒成立，则称为f（x）凹函数；若满足$f（\frac{{{x_1}+{x_2}}}{2}）$＞$\frac{{f（{x_1}）+f（{x_2}）}}{2}$恒成立，则称函数f（x）为凸函数，试证明：任一指数函数f（x）=ax（a＞0，a≠1）都是凹函数．
15．如图，一个平面图形的斜二测画法的直观图是一个边长为a的正方形，则原平面图形的面积为（　　）
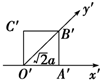
A．$\frac{\sqrt{2}}{4}$a2B．a2C．2$\sqrt{2}$a2D．2a2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网