Question

15．如图，一个平面图形的斜二测画法的直观图是一个边长为a的正方形，则原平面图形的面积为（　　）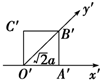

• A． $\frac{\sqrt{2}}{4}$a²
• B． a²
• C． 2$\sqrt{2}$a²
• D． 2a²

Answer 1

分析 由斜二测画法的规则知在已知图形平行于x轴的线段，在直观图中画成平行于x′轴，长度保持不变，已知图形平行于y轴的线段，在直观图中画成平行于y′轴，且长度为原来一半．由于y′轴上的线段长度为$\sqrt{2}$a，故在平面图中，其长度为2$\sqrt{2}$a，且其在平面图中的y轴上，由此可以求得原平面图形的面积．

解答 解：由斜二测画法的规则知与x′轴平行的线段其长度不变以及与横轴平行的性质不变，正方形对角线在y′轴上，
可求得其长度为$\sqrt{2}$a，故在平面图中其在y轴上，且其长度变为原来的2倍，长度为2$\sqrt{2}$a，
∴原平面图形的面积为$a•2\sqrt{2}a$=$2\sqrt{2}{a}^{2}$
故选：C．

点评 本题考查的知识点是平面图形的直观图，其中斜二测画法的规则，能够快速的在直观图面积和原图面积之间进行转化．