题目内容
20.判断下面命题的真值“|x︳>0”( )| A. | 假命题 | B. | 真命题 | C. | 不是命题 | D. | 可真可假 |
分析 举出反例x=0,可判断出“|x︳>0”为假命题.
解答 解:当x=0时,“|x︳=0”,
“|x︳>0”不成立,
故“|x︳>0”为假命题,
故选:A.
点评 本题考查的知识点是命题的真假判断与应用,难度不大,属于基础题.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
11.已知函数f(x)=$\left\{\begin{array}{l}{3x+1,x≤0}\\{|{x}^{2}-4x+1|.x>0}\end{array}\right.$,若函数g(x)=f2(x)-axf(x)恰有6个零点,则a的取值范围是( )
| A. | (0,3) | B. | (1,3) | C. | (2,3) | D. | (0,2) |
15.方程$(2x-y+2)\sqrt{{x^2}+{y^2}-1}=0$表示的曲线是( )
| A. | 一个点与一条直线 | B. | 两个点或一条直线或一个圆 | ||
| C. | 两个点 | D. | 两条射线和一个圆 |
12.正方体ABCD-A1B1C1D1中,E是棱BB1中点,G是DD1中点,F是BC上一点且FB=$\frac{1}{4}$BC,则GB与EF所成的角为( )
| A. | 30° | B. | 120° | C. | 60° | D. | 90° |
9.若函数f(x)=x2-x+1,x∈[-1,1],不等式f(x)>2x+m恒成立,则m的取值范围是( )
| A. | (-∞,-1) | B. | (-∞,3) | C. | (-1,3) | D. | (3,+∞) |
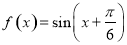 的图象上各点的纵坐标不变,横坐标扩大到原来的2倍,所得函数
的图象上各点的纵坐标不变,横坐标扩大到原来的2倍,所得函数 图象的一个对称中心可以是( )
图象的一个对称中心可以是( )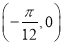 B.
B.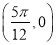 C.
C. D.
D.