题目内容
8.二项式(x+1)n(n∈N*)的展开式中x2的系数为15,则n=6.分析 在二项展开式的通项公式中,令x的幂指数等于2,求出n、r的关系,再根据展开式中x2的系数为15,求得n的值.
解答 解:二项式(x+1)n(n∈N*)的展开式的通项公式为Tr+1=${C}_{n}^{r}$•xn-r,
令n-r=2,求得r=n-2.
再根据${C}_{n}^{r}$=${C}_{n}^{n-2}$=${C}_{n}^{2}$=$\frac{n(n-1)}{2}$=15,求得n=6,
故答案为:6.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.判断下面命题的真值“|x︳>0”( )
| A. | 假命题 | B. | 真命题 | C. | 不是命题 | D. | 可真可假 |
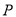 是圆
是圆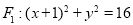 上任意一点(
上任意一点(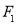 是圆心),点
是圆心),点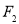 与点
与点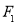 关于原点对称.线段
关于原点对称.线段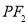 的中垂线
的中垂线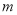 分别与
分别与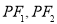 交于
交于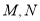 两点.
两点.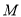 的轨迹
的轨迹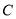 的方程;
的方程;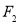 ,与抛物线
,与抛物线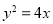 交于
交于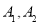 两点,与
两点,与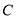 交于
交于 两点.当以
两点.当以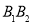 为直径的圆经过
为直径的圆经过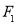 时,求
时,求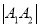 .
.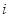 是虚数单位,
是虚数单位,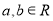 ,则“
,则“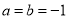 ”是“
”是“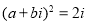 ”的( )
”的( )